Study of Elastic Anisotropy of Compounds RhBiX (X = Hf, Ti and Zr)

Sushil Rajpurohit

doi:10.61343/jcm.v3i02.99

Authors

Sushil Rajpurohit School of Science and Technology, Vardhman Mahaveer Open University, Kota, Rajasthan, India

DOI:

https://doi.org/10.61343/jcm.v3i02.99

Keywords:

Elastic, anisotropy, Young’s modulus, linear compressibility, shear modulus

Abstract

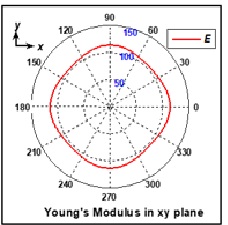
The study shows the minimum and maximum values of Young’s modulus, Poisson’s ratio and shear modulus of compounds RhBiHf, RhBiTi and RhBiZr at zero pressure using ELATE software. Anisotropy parameters A_Gand A^U for RhBiTi are slightly greater than the respective values of these parameters for RhBiHf and RhBiZr. The ratios of maximum to minimum values of Young’s modulus (E_max/E_min), linear compressibility (β_max/β_min), shear modulus (G_max/G_min) and Poisson’s ratio (ν_max/ν_min) for RhBiTi are 1.12, 1.00, 1.14 and 1.26, respectively. The investigation shows the spatial dependence of Young’s modulus, linear compressibility, Poisson’s ratio and shear modulus of compound RhBiTi through polar plots.

References

Wei, J., Yang, L., Ma, Z., Song, P., Zhang, M., Ma, J., Yang, F. and Wang, X., 2020. Review of current high-ZT thermoelectric materials. Journal of Materials Science, 55(27), pp.12642-12704.

https://doi.org/10.1007/s10853-020-04949-0

Fu, C., Bai, S., Liu, Y., Tang, Y., Chen, L., Zhao, X. and Zhu, T., 2015. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nature Communications , 6(1), p.8144.

https://doi.org/10.1038/ncomms9144

Zhu, H., Mao, J., Li, Y., Sun, J., Wang, Y., Zhu, Q., Li, G., Song, Q., Zhou, J., Fu, Y., He, R., Tong, T., Liu, Z., Ren, W., You, L., Wang, Z., Luo, J., Sotnikov, A., Bao, J., Nielsch, K., Chen, G., Singh, D.J. and Ren, Z., 2019. Discovery of TaFeSb-based half-Heuslers with high thermoelectric performance. Nature Communications, 10(1), p.270.

https://doi.org/10.1038/s41467-018-08223-5

Graf, T., Klaer, P., Barth, J., Balke, B., Elmers, H.J. and Felser, C., 2010. Phase separation in the quaternary Heusler compound CoTi(1− x)MnxSb–A reduction in the thermal conductivity for thermoelectric applications. Scripta Materialia, 63(12), pp.1216-1219.

https://doi.org/10.1016/j.scriptamat.2010.08.039

Wei, J., Guo, Y. and Wang, G., 2023. Exploring structural, mechanical, and thermoelectric properties of half-Heusler compounds RhBiX (X= Ti, Zr, Hf): A first-principles investigation. RSC Advances, 13(17), pp.11513-11524.

https://doi.org/10.1039/D3RA01262J

Blaha, P., Schwarz, K., Tran, F., Laskowski, R., Madsen, G.K.H. and Marks, L.D., 2020. WIEN2k: An APW+ lo program for calculating the properties of solids. The Journal of Chemical Physics, 152(7), p. 074101.

https://doi.org/10.1063/1.5143061

Carrete, J., Li, W., Mingo, N., Wang, S. and Curtarolo, S., 2014. Finding Unprecedentedly Low-Thermal-Conductivity Half-Heusler Semiconductors via High-Throughput Materials Modeling. Physical Review X, 4(1), p.011019. https://doi.org/10.1103/PhysRevX.4.011019

Feng, Z., Fu, Y., Zhang, Y. and Singh, D.J., 2020. Characterization of rattling in relation to thermal conductivity: Ordered half-Heusler semiconductors. Physical Review B, 101(6), p.064301.

https://doi.org/10.1103/PhysRevB.101.064301

Ma, J., Hegde, V.I., Munira, K., Xie, Y., Keshavarz, S., Mildebrath, D.T., Wolverton, C., Ghosh, A.W. and Butler, W.H., 2017. Computational Investigation of Half-Heusler Compounds for Spintronics Applications. Physical Review B, 95(2), p.024411.

https://doi.org/10.1103/PhysRevB.95.024411

Graf, T., Felser, C. and Parkin, S.S.P., 2011. Simple rules for the understanding of Heusler compounds. Progress in Solid State Chemistry, 39(1), pp.1-50.

https://doi.org/10.1016/j.progsolidstchem.2011.02.001

Kresse, G. and Hafner, J., 1993. Ab initio molecular dynamics for liquid metals. Physical Review B, 47(1), pp.558-561.

https://doi.org/10.1103/PhysRevB.47.558

Kresse, G. and Hafner, J., 1993. Ab initio molecular dynamics for open-shell transition metals. Physical Review B, 48(17), pp.13115-13118.

https://doi.org/10.1103/PhysRevB.48.13115

Kresse, G. and Hafner, J., 1994. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Physical Review B, 49(20), pp.14251-14269.

https://doi.org/10.1103/PhysRevB.49.14251

Kresse, G. and Furthmüller, J., 1996. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Physical Review B, 54(16), pp.11169-11186.

https://doi.org/10.1103/PhysRevB.54.11169

Kresse, G. and Furthmüller, J., 1996. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Computational Materials Science, 6(1), pp.15-50.

https://doi.org/10.1016/0927-0256(96)00008-0

Kresse, G. and Joubert, D., 1999. From ultrasoft pseudopotentials to the projector augmented-wave method. Physical Review B, 59(3), pp.1758-1775.

https://doi.org/10.1103/PhysRevB.59.1758

Hafner, J., 2008. Ab‐initio simulations of materials using VASP: Density‐functional theory and beyond. Journal of Computational Chemistry, 29(13), pp.2044-2078.

https://doi.org/10.1002/jcc.21057

Cramer, C.J., 2004. Essentials of Computational Chemistry: Theories and Models. 2nd ed. England: John Wiley & Sons Ltd.

Fermi, E., 1928. Eine statistische Methode zur Bestimmung einiger Eigenschaften des Atoms und ihre Anwendung auf die Theorie des periodischen Systems der Elemente. Zeitschrift für Physik, 48(1), pp.73-79.

https://doi.org/10.1007/BF01351576

Thomas, L.H., 1927. The calculation of atomic fields. Mathematical Proceedings of the Cambridge Philosophical Society, 23(5), pp.542-548.

https://doi.org/10.1017/S0305004100011683

Perdew, J.P., Burke, K. and Ernzerhof, M., 1996. Generalized Gradient Approximation Made Simple. Physical Review Letters, 77(18), pp.3865- 3868.

https://doi.org/10.1103/PhysRevLett.77.3865

Perdrew, J.P., Burke, K. and Ernzerhof, M., 1997. Erratum: Generalized Gradient Approximation Made Simple [Physical Review Letters, 77, 3865 (1996)]. Physical Review Letters, 78(7), p.1396.

https://doi.org/10.1103/PhysRevLett.78.1396

Voigt, W., 1928. Lehrbuch der Kristallphysik. BG Teubner, Leipzig und Berlin.

Reuss, A. and Angew, Z., 1929. Berechnung der Fliesgrenze von Mischkristallen auf Grund der Plastizatsberechnung fur Einkristalle. Journal of Applied Mathematics and Mechanics, 9(1), pp.49–58.

https://doi.org/10.1002/zamm.19290090104

Hill, R., 1952. The Elastic Behaviour of a Crystalline Aggregate. Proceedings of the Physical Society, Section A, 65(5), p.349-354. https://doi.org/10.1088/0370-1298/65/5/307

Gaillac, R., Pullumbi, P. and Coudert, F.X., 2016. ELATE: An open-source online application for analysis and visualization of elastic tensors. Journal of Physics: Condensed Matter, 28(27), p.275201.

https://doi.org/10.1088/0953-8984/28/27/275201

http://progs.coudert.name/elate

Nye, J.F., 1985. Physical Properties of Crystals: Their Representation by Tensors and Matrices. New York: Oxford University Press Inc.

Chung, D.H. and Buessem, W.R., 1967. The Elastic Anisotropy of Crystals. Journal of Applied Physics, 38(5), pp.2010-2012.

https://doi.org/10.1063/1.1709819

Chung, D.H. and Buessem, W.R., 1968. Anisotropy in Single Crystal Refractory Compounds: Vol. 2. (Eds. Vahldiek, F.W. and Mersol, S.A.), New York: Plenum Press. pp. 217–246

Ranganathan, S.I. and Ostoja-Starzewski, M., 2008. Universal Elastic Anisotropy Index. Physical Review Letters, 101(5), p.055504.

https://doi.org/10.1103/PhysRevLett.101.055504

Marmier, A., Lethbridge, Z.A.D., Walton, R.I., Smith, C.W., Parker, S.C. and Evans, K.E., 2010. ElAM: A computer program for the analysis and representation of anisotropic elastic properties. Computer Physics Communications, 181(12), pp.2102-2115.

https://doi.org/10.1016/j.cpc.2010.08.033.