Design of Linear Magnetic Field Sensor Based on Periodically Magnetized Cold Plasma
Nisha1, Kumar N2, Suthar B3*
DOI:10.61343/jcm.v1i01.4
1 Nisha, Department of Physics, SLAS Mody University of Science and Technology, Lakshmangarh 332311 Sikar , Rajasthan, India.
2 Narendra Kumar, Department of Physics, SLAS Mody University of Science and Technology, Lakshmangarh 332311 Sikar, Rajasthan, India.
3* Bhuvneshwer Suthar, Department Of Physics, Govt Dungar College, Bikaner 334001, Rajasthan, India.
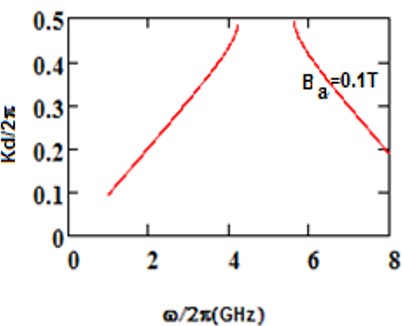
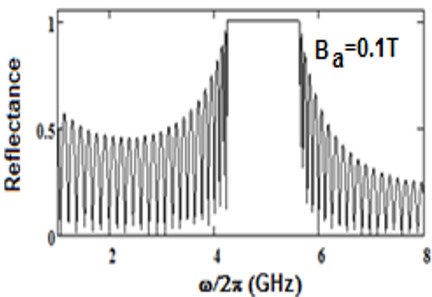
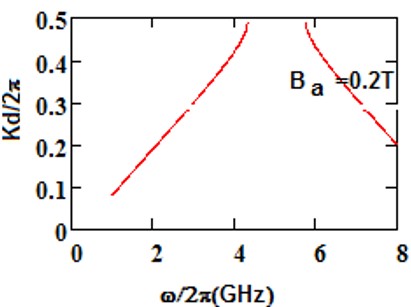
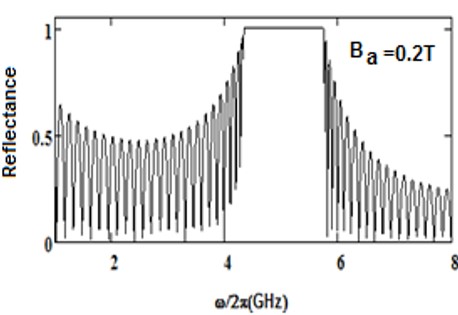
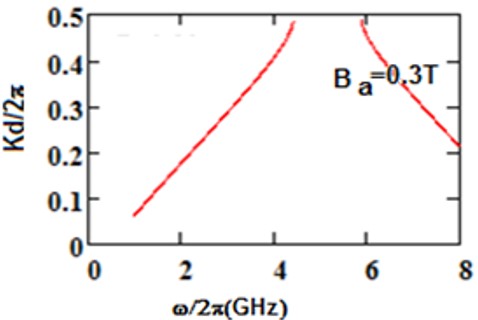
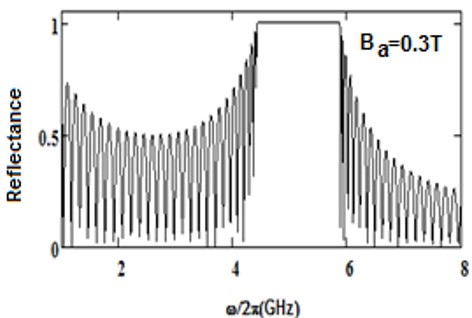
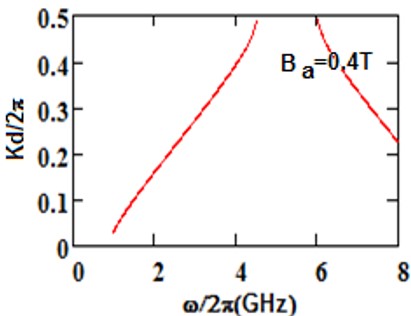
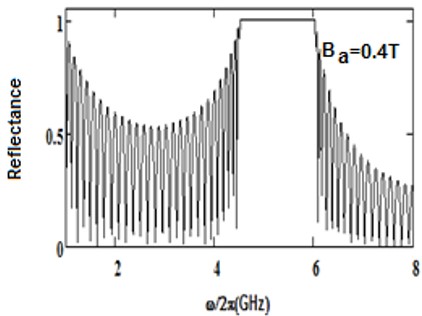
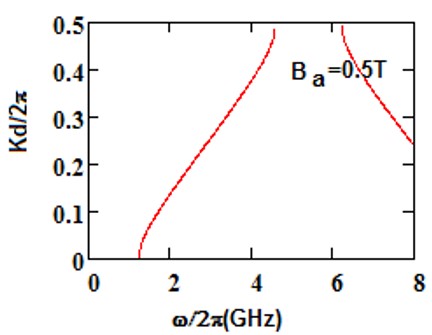
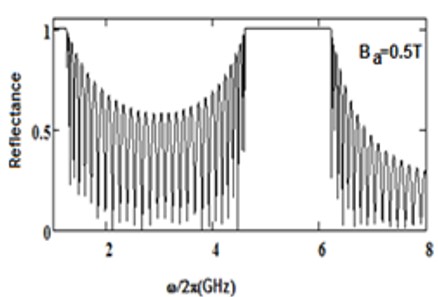
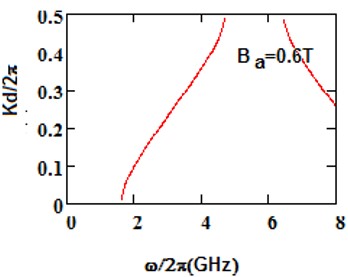
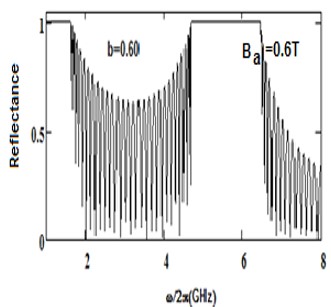
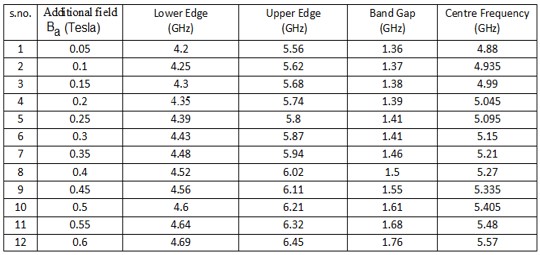
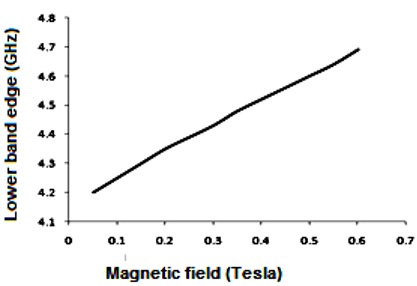
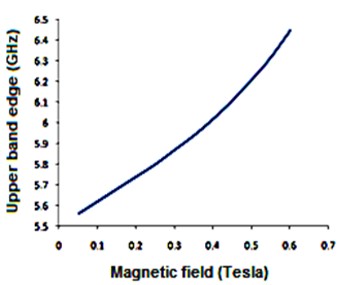
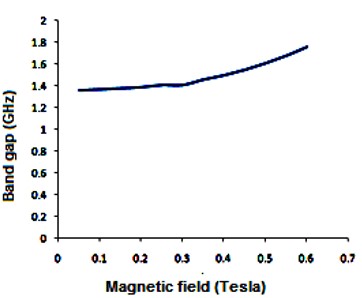
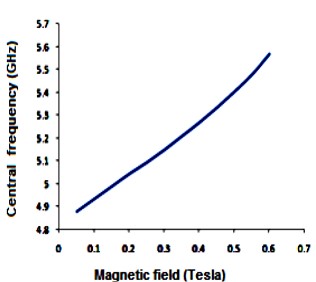
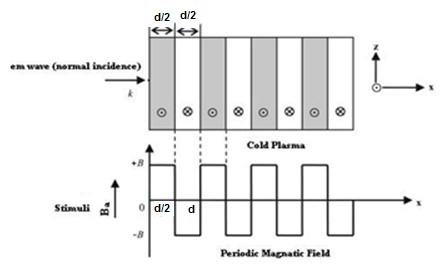
We have analyzed the impact of a linear magnetic field on the photonic band gaps exhibited by bulk cold plasma, under external square-wave-like periodic magnetic field of fixed magnitude, conceived as an extrinsic photonic crystal. Here photonic band gaps are determined using transfer matrix method (TMM). Here, the impact of an additional linear magnetic field is determined on the band gaps of plasma photonic crystal with constant magnitude of square like periodic magnetic field, for normal incidence. We determine how the additional and magnetic magnetic field affects the photonic band structure (PBS) and reflectance for such extrinsic photonic crystal. It is noted that, as we increase the additional applied magnetic field, the central frequency of band gaps is shifted toward higher frequency regions in GHz. The band edge increases linearly with the applied magnetic field. The shifting in lower band edge less as compared to upper edge. Sensor is a device which detect the stimuli and give output, and many physical parameters can be measured by sensors. The shifting of band edges can be utilized in design of magnetic field sensor. Here shifting in band gaps by variation in the additional applied magnetic field are determined. The larger value of sensitivity gives a good result for sensing-based application. This analysis is based on the band gaps of extrinsic photonic crystal, and can be employed in design of magnetic field sensor with good sensitivity. Moreover, it can find applications in tunable optical devices.
Keywords: Extrinsic, Magnetized, Magnetic field, Sensor, Reflectance, Cold plasma, Photonic crystals
| Corresponding Author | How to Cite this Article | To Browse |
|---|---|---|
| , , Department Of Physics, Govt Dungar College, Bikaner 334001, Rajasthan, India. Email: |
Nisha, Kumar N, Suthar B, Design of Linear Magnetic Field Sensor Based on Periodically Magnetized Cold Plasma. J.Con.Ma. 2023;1(1):16-23. Available From https://jcm.thecmrs.in/index.php/j/article/view/4 |


 ©
© 
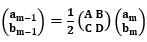 (1)
(1)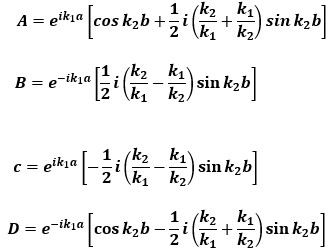
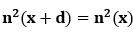 (2)
(2)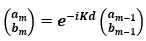 (3)
(3)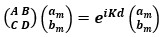 (4)
(4)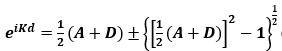 (5)
(5)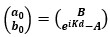 (6)
(6)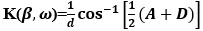 (7)
(7)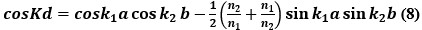 (8)
(8)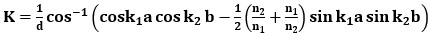 (9)
(9)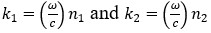
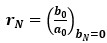 (10)
(10)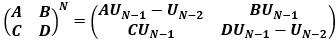 (11)
(11)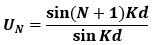
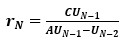 (12)
(12)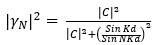 (13)
(13)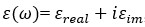 , where ∈ is the dielectric constant and ⍵ is the angular wave frequency
, where ∈ is the dielectric constant and ⍵ is the angular wave frequency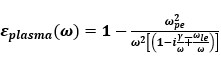 (14)
(14)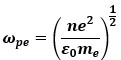
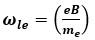
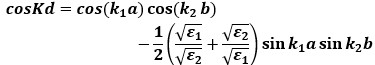
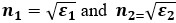 .
.