E-ISSN:2583-9152

Research Article

Material Science

Journal of Condensed Matter

2023 Volume 1 Number 2 Jul-Dec
Publisherwww.thecmrs.in

Ab Initio Study of Structural and Magnetic Properties of Cobalt Doped Zinc Oxide

Sharmaa Y1, Heera P2*
DOI:10.61343/jcm.v1i02.36

1 Yojana Sharmaa, Department Of Physics Astronomical Science, Central University Of Himachal Pradesh176206, HP, India.

2* Pawan Heera, Department Of Physics Astronomical Science, Central University Of Himachal Pradesh176206, HP, India.

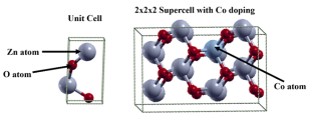
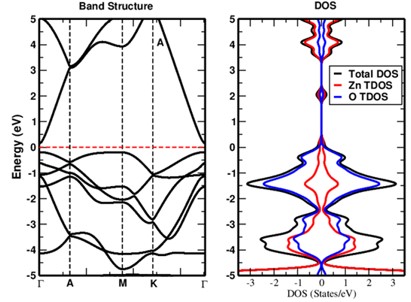
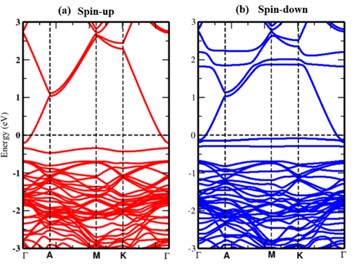
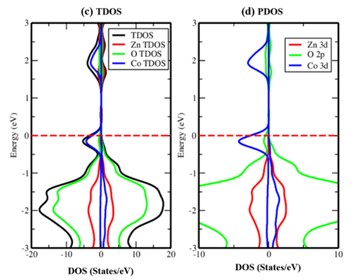
In this study, we have investigated the electronic and magnetic properties of Cobalt doped zinc oxide (ZnO) bulk materials using density functional theory (DFT) calculations. The substitution of Co atoms into the ZnO lattice is systematically explored to understand its impact on the electronic band structure, magnetic moments and stability of the material. It is observed that Co doping introduces localized magnetic moments of 3.073 μB associated with Co atoms. The electronic band structure exhibits the semi-metallic nature after the Co doping with a majority spin (↑) and a minority spin (↓) magnetic configuration hybridization between Co 3d and 2p orbitals of O, indicating the potential for spin-polarized transport in Co-doped ZnO. We have also analyzed the formation energies to assess the thermodynamic stability. It is observed that the binding energy per atom slightly decreased to -3.563 eV, indicating stable Co incorporation. From the obtained results it can be concluded that, through controlled doping strategies the electronic and magnetic properties in ZnO-based materials can be altered for desired properties.

Keywords: Band Structure, Magnetic Moment, DFT (Density Functional Theory), Thermodynamic Stability, ZnO

Corresponding Author How to Cite this Article To Browse
Pawan Heera, , Department Of Physics Astronomical Science, Central University Of Himachal Pradesh176206, , HP, India.
Email: 		Sharmaa Y, Heera P, Ab Initio Study of Structural and Magnetic Properties of Cobalt Doped Zinc Oxide. J.Con.Ma. 2023;1(2):118-122.
Available From
https://jcm.thecmrs.in/index.php/j/article/view/36

Manuscript Received Review Round 1 Review Round 2 Review Round 3 Accepted
2023-11-10 2023-11-15 2023-11-20 2023-11-25 2023-12-01
Conflict of Interest Funding Ethical Approval Plagiarism X-checker Note
None Nil Yes 18.98%

© 2023by Sharmaa Y, Heera Pand Published by Condensed Matter Research Society. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/ unported [CC BY 4.0].

J.Con.Ma 2023;1(2)118
Y Sharma et al.: Ab Initio Study of Structural and Magnetic Properties of Cobalt Doped ZnO

Introduction

In recent years, the concept of simultaneously manipulating both electric charge and electrons spin in nanomaterials has generated substantial interest in the domain of spintronics. The primary goal is to create a semiconductor based ferromagnet whose properties can be precisely controlled at room temperature, which in turn will explore possibilities for magnetoelectric and magneto transport related devices [1]. Typically, intrinsic magnetic semiconductors have relatively low Curie temperatures (TC), which restrict their practical utility. However, researchers have proposed a solution by introducing transition metal or rare earth ions into a nonmagnetic semiconductor host lattice [2]. This process results in a dilute magnetic semiconductor (DMS), with the potential to raise TC to levels suitable for room temperature operation [3-4].

In DMS materials, the magnetism is closely linked to the existence of charge carriers, which can take the form of either holes (as seen in materials like GaAs: Mn) or electrons (as seen in materials like GaN:Gd). However, there is an ongoing debate about the underlying process accounting for the high-temperature magnetic alignment observed in these systems. This debate is further complicated by significant discrepancies between results obtained in experimental and theoretical studies [5-8].

ZnO, an n-type semiconductor with a wide bandgap, has gained significant attention both experimentally as well as theoretically in recent years. This renewed interest stems from the pioneering work of Dietl et al. and Ueda et al. [9, 10], who suggested that ZnO doped with transition metals (TMs) could potentially serve as a DMS suitable for spintronic applications at room temperature. This prediction ignited a flurry of experimental efforts to realize room temperature ferromagnetism in transition metals doped ZnO. However, the quest for achieving this ferromagnetism has been met with significant controversy, with the success often hinging on the specific methods employed for sample preparation [11-13]. Recent studies on gallium and cobalt-codoped ZnO have underscored the contribution of gallium ions situated in octahedral interstitial sites and the presence of oxygen vacancies in enabling ferromagnetism at room

temperature [14]. Interestingly, even nonmagnetic Co-doped ZnO has exhibited ferromagnetic behavior when codoped with lithium [15], while co-doping with aluminium has yielded contrasting experimental results [16-17]. The cobalt and copper codoped ZnO system has also demonstrated ferromagnetic properties [18-19].

In particular, we are motivated by the intriguing observations mentioned above, both theoretical and experimental, regarding TMs doped (i.e., Al, Fe, Co) ZnO systems. In this study, we conduct a comprehensive examination of magnetic behaviour of the Co-doped ZnO system. These calculations shows that the critical role of defects in promoting magnetism in the codoped system.

Methodology

Here we have focused on performing electronic structure calculations using advanced first-principles techniques, particularly within the framework of Density Functional Theory (DFT). To carry out these intricate calculations, we have used the SIESTA (Spanish Initiative for Electronic Simulation with Thousands of Atoms) code [20]. To accurately capture the interactions among electrons within our systems, we employed the GGA-PBE functional, a computational tool that helps in describing these complex electron-electron interactions with threshold less than 0.001 eV/Å per atoms and energy shift of 20 meV. We have used a mesh cutoff energy of 300 Ry to ensure precision and considering the Brillouin zone integration 15 x 15 x 1 Monkhorst pack grid [21].

jcm_36_01.jpg
Figure 1: Supercell with 32 atoms

Results And Discussions

ZnO bulk nanostructure adopts a wurtzite crystal arrangement (Fig. 1), which is a hexagonal analog of the zinc-blende lattice and belongs to the P63mc space group which contains two Zn and O atoms within each unit cell as shown in Fig.1. The optimized lattice constant for pristine


J.Con.Ma 2023;1(2)119
Y Sharma et al.: Ab Initio Study of Structural and Magnetic Properties of Cobalt Doped ZnO

bulk is, a = 2.903 Å, b = 3.085 Å and c = 5.283 Å. For doping of Cobalt, we have employed a 2x2x2 supercell configuration, encompassing 32 atoms (Fig.1). Within this supercell, the replacement of a single Zn atom with a Co atom equates to a dopant concentration of 6.25%. With the doping of Co, the optimized lattice constant is found to increase (Table 1). Moreover, in comparison with pristine, Co doped ZnO supercell resulted in an increase of crystallite size due to the difference in ionic radii of Co2+ and Zn2+. It suggests that the Co2+ ions have replaced the Zn2+ ions within the structure without causing any deformation to the ZnO structure. Such type of behaviour can be understood by considering the Co2+ ions which tend to naturally adopt an octahedral arrangement within the wurtzite structure. Jayakumar O.D et.al. [22] has highlighted that Co2+ ions possess varying radii depending on their spin state, ranging from 0.65 Å (in the low spin state) to 0.745 Å (in the high spin state). In contrast, Zn2+ ions typically assume a tetrahedral coordination with an approximate radius of 0.60 Å. As a result, the slight expansion of the Lattice Constants can be attributed to the Co2+ ions taking up positions within the crystal structure where they form octahedral coordination and effectively replace Zn2+ ions within the ZnO nanostructures.

Further, we have calculated the binding energy using [23], in order to investigate the structural stability. The calculated binding energy for Pristine ZnO is found to be -3.462 eV/atoms while it increases to -3.563 eV/atoms when Cobalt is doped, resulting into further stability of Co doped crystal as compared to pristine ZnO. The computed band structure of pristine ZnO, with the reference point designating the Fermi level as zero (red dotted line in Fig. 2 (band structure)), reveals two critical regions; the conduction band above and the valence band below (Fig. 2). These bands intersect at the same k-point, marked as Г, indicating that ZnO possesses the characteristic of being a direct gap semiconductor. The calculated value of band gap for pure ZnO is found to be 0.342 eV which is in agreement the literature [24]. However, it is worth noting that this computed value is significantly smaller than the experimental measurement of 3.2 eV, such deviations may be due to the calculations using the LDA or GGA methods [25]. Our calculations yielded a significantly lower band gap which can be attributed to certain limitations of the Density Functional Theory (DFT)

within the Generalized Gradient Approximation (GGA), especially when applied to transition metal oxides like ZnO [21].

In Fig. 3 (c) & (d), a comprehensive view of the total Density of States (DOS) and the Partial Density of States of Co doped ZnO, specifically focusing on the Zn-d and Co-d orbitals which encompass Ferrimagnetic (FI) configurations. In the absence of any structural defects within the pristine ZnO system, the d orbitals associated with Co, which are separated by 3.25 Å in a crystal field characterized by tetrahedral symmetry, undergoes a process called orbital splitting [23]. This splitting leads to the emergence of two distinct sets of states spin-up and spin-down. It is expected that the transition metal (TM) ions exclusively occupy substitutional positions at the Zn site, leading to an expected oxidation state of 2+ for Co. Under a spin-polarized condition, the system exhibits a preference

Table 1: Optimized parameter of pristine ZnO and Cobalt doped ZnO

StructureLattice Constant (Å)Binding Energy (eV/atom)Magnetic Moment (μB)Band Gap (eV)Bond Length (Å)
ZnO pristine (Unit Cell)a = 2.903b = 3.085 c = 5.283  −3.462  0.000  0.342  Zn-O = 2.06
Co doped ZnO at Zn Site (2x2x2)a = 5.861b = 6.006 c = 10.577  −3.563  3.073 Half metal  Zn-O = 2.09 Co-O = 2.11

jcm_36_02.jpg
Figure 2: Band structure and total density of states (TDOS) of pristine ZnO

for a high-spin configuration. The Co doing, which possesses a d7 configuration, the majority spins (spin-up), is completely filled with d↓5 electrons (Fig. 3 (c) & (d) shown as blue coloured lines), while the minority spin channel (spin-down), is only half-filled. The total Density of States


J.Con.Ma 2023;1(2)120
Y Sharma et al.: Ab Initio Study of Structural and Magnetic Properties of Cobalt Doped ZnO

(DOS) and Partial DOS presented in Fig.3 (c) & (d) accurately depict the distribution of electrons as described above. As expected, the Ferrimagnetic (FI) state introduces a reversal in the occupancies of Co in both the up and down spin channels and adopts the configuration of d↓5, aligning with the electron distribution characteristic of the Ferrimagnetic state. For our study, the primary focus was to explore the influence of cobalt (Co) content on the band structure of Co-doped ZnO.

jcm_36_03.jpg
jcm_36_03.jpg
Figure 3: Band structure of Co doped ZnO (a) Spin-up, (b) Spin-down, (c) TDOS and (d) PDOS of each atom

Conclusions

In this work, the primary focus was to explore the influence of cobalt (Co) content on the band structure of ZnO. We observed that pristine ZnO is a direct band gap semiconductor with energy band gap of 0.342 eV. With the Cobalt doping the structure becomes more stable with a binding energy of -3.563 eV as compared to pristine ZnO. Moreover, the doping of

Co enhanced the spin polarized states by removing the spin degeneracy near Fermi energy. Band structure and total density of states of Co doped ZnO exhibit both spin up and spin down states near Fermi energy. Partial DOS of both spin up and spin down states shows that the contribution of down spin states to the magnetic behavior is more. Therefore, Cobalt doped ZnO is promising material for spintronics.

Acknowledgments

The authors extend their appreciation to the SIESTA for providing the open-source code. Further, Yojana Sharma is thankful to Mr. Narender Kumar from the Department of Physics at the United Arab Emirates University for his invaluable assistance in setting up the SIESTA code and for furnishing the necessary scripts for result analysis.

References

1. D. D. Awschalom and M. E. Flatte, Nature Phys. 3, 153 (2007).

2. Pratap, Surender, et al. "Recent development of two-dimensional tantalum dichalcogenides and their applications", Micro and Nanostructures (2023): 207627.

3. T. Dietl et al., Science 287, 1019 (2000).

4. K. Sato and H. Katayama-Yoshida, Semicond. Sci.Technol. 17, 367 (2002).

5. R. Janisch, P. Gopal, and N. A. Spaldin, J. Phys. Condens.Matter 17, R657 (2005).

6. P. Gopal and N. A. Spaldin, Phys. Rev. B 74, 094418(2006).

7. E.-J. Kan et al., J. Appl. Phys. 102, 033915 (2007).

8. C. H. Patterson, Phys. Rev. B 74, 144432 (2006).

9. T. Dietl, H. Ohno, F. Matsukura, J. Cibert, and D. Ferrand, Science 287, 1019 (2000).

10. K. Ueda, H. Tabata, and T. Kawai, Appl. Phys. Lett. 79, 988 (2001).

11. Y. Fukuma, F. Odawara, H. Asada, and T. Koyanagi, Phys. Rev. B 78, 104417 (2008).

12. G. S. Chang, E. Z. Kurmaev, D. W. Boukhvalov, L. D. Finkelstein, S. Colis, T. M. Pedersen,


J.Con.Ma 2023;1(2)121
Y Sharma et al.: Ab Initio Study of Structural and Magnetic Properties of Cobalt Doped ZnO

A. Moewes, and A. Dinia, Phys. Rev. B 75, 195215 (2007).

13. D. Rubi, J. Fontcuberta, A. Calleja, L. Aragonès, X. G. Capdevila, and M. Segarra, Phys. Rev. B 75, 155322 (2007).

14. Y. He, P. Sharma, K. Biswas, E. Z. Liu, N. Ohtsu, A. Inoue, Y. Inada, M. Nomura, J. S. Tse, S. Yin, and J. Z. Jiang, Phys. Rev. B 78, 155202 (2008).

15. M. H. F. Sluiter, Y. Kawazoe, P. Sharma, A. Inoue, A. R. Raju, C. Rout, and U. V. Waghmare, Phys. Rev. Lett. 94, 187204 (2005).

16. X. C. Liu, E. W. Shi, Z. Z. Chen, H. W. Zhang, B. Xiao, and L. X. Song, Appl. Phys. Lett. 88, 252503 (2006).

17. D. Iusan, R. Knut, B. Sanyal, O. Karis, O. Eriksson, V. A. Coleman, G. Westin, J. M. Wikberg, and P. Svedlindh, Phys. Rev. B 78, 085319 (2008).

18. N. N. Lathiotakis, A. N. Andriotis, and M. Menon, Phys. Rev. B 78, 193311 (2008).

19. M. S. Park and B. I. Min, Phys. Rev. B 68, 224436 (2003).

20. Soler, José M., et al. "The SIESTA method for ab initio order-N materials simulation." Journal of Physics: Condensed Matter 14.11 (2002): 2745.

21. Mostofi, Arash A., et al. "wannier90: A tool for obtaining maximally-localisedWannier functions." Computer physics communications 178.9 (2008): 685-699.

22. Jayakumar, O. D., I. K. Gopalakrishnan, and S. K. Kulshreshtha. "The structural and magnetization studies of Co-doped ZnO co-doped with Cu: Synthesized by co-precipitation method", Journal of Materials Chemistry 15.34 (2005): 3514-3518

23. Devi, Anjna, et al. "Electronic Band Gap Tuning and Calculations of Mechanical Strength and Deformation Potential by Applying Uniaxial Strain on MX2 (M= Cr, Mo, W and X= S, Se) Monolayers and Nanoribbons", ACS omega 7.44 (2022): 40054-40066.

24. Paudel, Tula R., and Walter RL Lambrecht. "First-principles calculation of the O vacancy in ZnO: A self-consistent gap-corrected approach", Physical Review B 77.20 (2008): 205202.

25. Lany, Stephan, and Alex Zunger, "Assessment

of correction methods for the band-gap problem and for finite-size effects in supercell defect calculations: Case studies for ZnO and GaAs", Physical Review B 78.23 (2008): 235104.


J.Con.Ma 2023;1(2)122