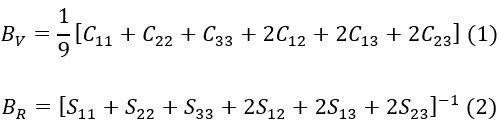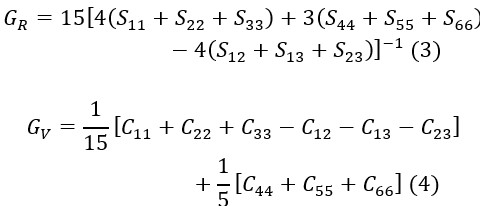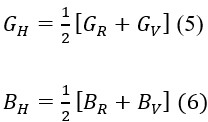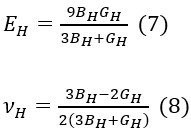E-ISSN:2583-9152

Research Article

Material Science

Journal of Condensed Matter

2023 Volume 1 Number 2 Jul-Dec
Publisherwww.thecmrs.in

Ab-initio Investigation of Elastic Properties of Monoclinic ZnAs2 Crystal

Rajpurohit S1*, Sharma G2
DOI:10.61343/jcm.v1i02.34

1* S Rajpurohit, School Of Science And Technology, Vardhman Mahaveer Open University, Kota 324010, India.

2 G Sharma, Department of Pure and Applied Physics, University of Kota, Kota 324005, India.

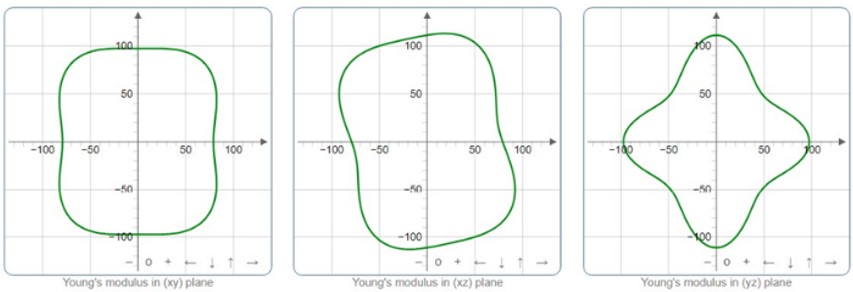
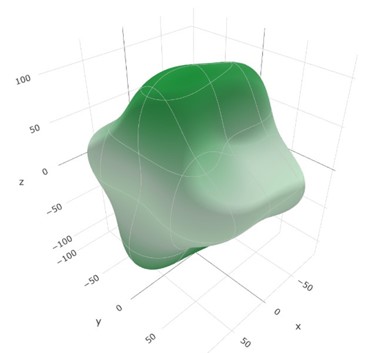
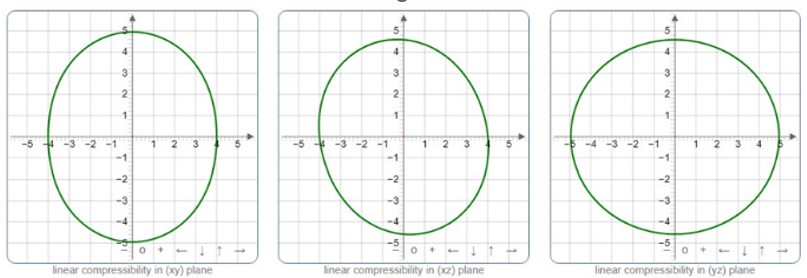
Elastic properties of monoclinic ZnAs2 crystal are studied under the PBEsol scheme using the CRYSTAL Program. Independent elastic stiffness coefficients have been computed. Various elastic properties, such as shear modulus, bulk modulus, Young’s modulus and Poisson’s ratio have been analyzed. The directional dependence of the computed Young’s modulus and linear compressibility is studied using ELATE software. Our investigation reveals the finite elastic anisotropy of the monoclinic ZnAs2 crystal.

Keywords: ZnAs2, Ab-initio, Elastic properties, Elastic anisotropy

Corresponding Author How to Cite this Article To Browse
S Rajpurohit, , School Of Science And Technology, Vardhman Mahaveer Open University, Kota 324010, , India.
Email: 		Rajpurohit S, Sharma G, Ab-initio Investigation of Elastic Properties of Monoclinic ZnAs2 Crystal. J.Con.Ma. 2023;1(2):128-132.
Available From
https://jcm.thecmrs.in/index.php/j/article/view/34

Manuscript Received Review Round 1 Review Round 2 Review Round 3 Accepted
2023-11-05 2023-11-12 2023-11-17 2023-11-23 2023-12-01
Conflict of Interest Funding Ethical Approval Plagiarism X-checker Note
None Nil Yes 18.95

© 2023by Rajpurohit S, Sharma Gand Published by Condensed Matter Research Society. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/ unported [CC BY 4.0].

J.Con.Ma 2023;1(2)128
S Rajpurohit et al: Ab-initio Investigation of Elastic Properties of Monoclinic ZnAs2 Crystal

Introduction

Monoclinic ZnAs2 is a semiconducting compound of the II-V group [1]. ZnAs2 has a monoclinic crystal structure with space group P21/c () [2-3]. Its unit cell has eight formula units [2]. The energy band gap is nearly 1eV [4-5]. There is tetrahedral coordination of atoms with a slight distortion of the tetrahedral structure [6]. ZnAs2 crystals are useful for optoelectronic applications, such as light modulators, optical filters, lenses, etc. [7]. Anisotropy in the thermoelectric power of these crystals is useful for nonselective radiation detectors [8]. Soshnikov et al studied the elastic properties of ZnAs2 crystals with ultrasound measurements [9]. These crystals may be utilized for the fabrication of polarization-controlled switches due to their polarization photosensitivity [10]. Photosensitive Schottky barriers may be formed on monoclinic ZnAs2 crystals [10]. The variation of index of refraction of ZnAs2 crystal may be utilized in fabricating infrared polarizers [11-12]. Our interpretation of the elastic properties of ZnAs2 may have considerable practical utility in device design for future research. For optimum performance of the device, knowledge of the direction-dependent elastic anisotropy of ZnAs2 crystals provides advantages in determining the preferred orientation of the crystals.

Computational details

Ab-initio investigation of monoclinic ZnAs2 is performed with CRYSTAL Code [13-14]. In the present study, the DFT exchange-correlation functional GGA is employed. The basis sets for Zn and As atoms have been utilized from the CRYSTAL-Basis Set Library [13-14]. Using initial geometry [3], optimization is performed and optimized lattice parameters and fractional coordinates are obtained. In this computation, the PBEsol [15] technique is implemented. The SCF convergence TOLDEE is set to 8. The calculations are performed using an 8 × 8 × 8 Monkhorst-Pack k-point mesh [16]. This k-point mesh corresponds to 125 k-points in the irreducible Brillouin zone. The BROYDEN parameter [13-14, 17-18] is also implemented to obtain convergence. The elastic properties [19-20] are studied at the equilibrium volume with a strain step of 0.01. The ELASTCON keyword is used for the computation of the elastic properties of monoclinic ZnAs2 crystals. ELATE software [21-22] is used for the analysis of elastic quantities.

Results and Discussion

Elastic Properties

The analysis of elastic anisotropy is useful for understanding the direction-dependent elastic stretchability of crystals. This analysis is useful for engineering device design. The monoclinic crystal system has thirteen independent elastic stiffness constants [23]. Using the initial geometry [3] with lattice parameters a = 9.287 Å, b = 7.691 Å, c = 8.010 Å, optimized lattice parameters have been obtained by CRYSTAL Code [13-14]. Using the optimized lattice parameters and fractional coordinates, the elastic stiffness constants of the monoclinic ZnAs2 crystal are obtained, which are shown in table 1.

Table 1: Elastic stiffness constants (in GPa) of ZnAs2 at zero pressure.

 SchemeC11C12C13C15C22C23C25C33C35C44C46C55C66
Present WorkPBEsol126.7263.4759.954.41136.8138.356.07145.841.7526.734.2344.5844.18
Other Worka 95.6331.47  102.5  112.6 20.76  40.45

aRef. [9, 24].

Table 2. Computed valuesb of shear modulus G (in GPa), bulk modulus B (in GPa), Young’s modulus E (in GPa) and Poisson’s ratio  (unitless) of ZnAs2.

 BVBRBHGVGRGHEVEREHVVVRVH
Present Workb81.4481.2881.3639.6036.6738.14102.2495.6398.950.2910.3040.297

 b Values of B, G, E and  have been computed with the help of ELATE software [21, 22]

Table 3. Variationsc of Young’s modulus E (in GPa), shear modulus G (in GPa), Poisson’s ratio  (unitless) and linear compressibility b [in ] of ZnAs2.

  Gmin  Gmax  Emin Emaxβminβmax  VminVmax
Present Work25.7651.7670.92121.473.604.450.0510.491

cThese values of G, E, b and  have been computed through ELATE software.

Table 1 shows that the elastic constant C33 is greater than other elastic constants. It is obvious from table 1 that the value of C22 is greater than C11 at zero pressure. Elastic stiffness constants C44 and C66 are significantly smaller than the other elastic stiffness constant C11.

Voigt bulk modulus (BV) and Reuss bulk modulus (BR) may be represented as a function of elastic


J.Con.Ma 2023;1(2)129
S Rajpurohit et al: Ab-initio Investigation of Elastic Properties of Monoclinic ZnAs2 Crystal

stiffness constants Cij and elastic compliance constants Sij [25, 26]

jcm_34_1_a.jpg

Reuss shear modulus (GR) and Voigt shear modulus (GV) are represented by [25, 26]

jcm_34_2.jpg

The Voigt-Reuss-Hill approximation provides the estimated polycrystalline shear (GH) and bulk moduli (BH) [25-27]

jcm_34_3.jpg

Also, macroscopic polycrystalline Poisson’s ratio VH and Young’s modulus EH may be represented as follows [25-27]:

jcm_34_4.jpg

The computed elastic moduli from elastic constants are shown in table 2.

The malleable property of a polycrystalline substance is expected to have a ratio of bulk modulus to shear modulus greater than about 1.75 [28]. The obtained value of Young’s modulus shows sufficient stiffness of ZnAs2. The value of 81.36 GPa of bulk modulus shows the ample material strength of ZnAs2 crystals under deformation. The computed value of 0.297 of Poisson’s ratio is within the theoretical limits [29] for materials. Maximum and minimum values of Young’s modulus, shear modulus, Poisson’s ratio and linear compressibility of ZnAs2 are shown in table 3.

The elastic anisotropy of a crystal may be expressed as [30, 31]

jcm_34_5.jpg

The calculated values of anisotropy parameters AB and AG are 0.00098 and 0.0384 respectively.

Ranganathan et al [32] expressed the universal elastic anisotropy index in the following manner:

jcm_34_6.jpg

The obtained value of Ranganathan’s universal elastic anisotropy index for ZnAs2 is 0.402. All these finite values of anisotropy parameters indicate the presence of finite anisotropy in ZnAs2 crystals. For isotropic materials, the value of each of the anisotropy parameters AB, AG and AU is zero. With the help of ELATE software [21-22], the directional dependence of Young’s modulus E and linear compressibility β is plotted in figures 1, 2 and 3. It is evident from figures 1 and 2 that directional Young’s modulus has anisotropy. Similarly, figures 3 and 4 show the sufficient anisotropy of linear compressibility in ZnAs2 crystal.

jcm_34_7.jpg
Figure 1. Directional dependence of the Young’s modulus E (in GPa) of ZnAs2

jcm_34_8.jpg
Figure 2. 3D View of the directional Young’s modulus E (in GPa) of ZnAs2


J.Con.Ma 2023;1(2)130
S Rajpurohit et al: Ab-initio Investigation of Elastic Properties of Monoclinic ZnAs2 Crystal

jcm_34_9_a.jpg
Figure 3. Directional dependence of the computed linear compressibility β [in ] of ZnAs2

jcm_34_10.jpg
Figure 4. 3D View of the directional linear compressibility β [in ] of ZnAs2

Conclusion

The investigation reveals the various elastic properties of ZnAs2 by using the GGA-PBEsol functional in the CRYSTAL program. Our investigation predicts the malleable nature of ZnAs2. In the present findings, the obtained value of Ranganathan’s universal elastic anisotropy index for ZnAs2 is 0.402. It can be concluded from the study that ZnAs2 has definite elastic anisotropy. Our present findings show that variation in the value of Young’s modulus from its minimum value to its maximum value is 50.55 GPa. For the shear modulus, the variation in the value from minimum to maximum is 26 GPa. Our investigation of the anisotropic properties of ZnAs2 may shed light on the preferred orientation of crystals for designing engineering devices using ZnAs2 crystals.

References

1. Weszka J, Mazurak Z and Pishchikov D I 1992 phys. stat. sol. (b) 170 89-92. https://doi.org/10.1002/pssb.2221700110

2. Senko M E, Dunn H M, Weidenborner J and Cole

H 1959 Acta Crystallogr. 12 76 https://doi.org/10.1107/S0365110X59000214

3. Fleet M E 1974 Acta Crystallogr. B 30 122-6. https://doi.org/10.1107/S0567740874002329

4. Turner W J, Fischler A S and Reese W E 1961 Phys. Rev. 121 759-67 https://doi.org/10.1103/PhysRev.121.759

5. Madelung O 2004 Semiconductors: Data Handbook Springer-Verlag Berlin Heidelberg

6. Weszka J, Balkanski M, Jouanne M, Pishchikov D I and Marenkin S F 1992 phys. stat. sol. (b) 171 275-81 https://doi.org/10.1002/pssb.2221710130

7. Matveeva L A and Matiyuk I M 2001 Proc. SPIE Eighth International Conference on Nonlinear Optics of Liquid and Photorefractive Crystals 4418 44180X https://doi.org/10.1117/12.428319

8. Morozova V A, Marenkin S F and Koshelev O G 2002 Inorg. Mater. 38 325-30. https://doi.org/10.1023/A:1015137301787

9. Soshnikov L E, Trukhan V M, Haliakevich T V and Soshnikava H L 2005 Mold. J. Phys. Sci. 4 201–10

10. Nikolaev Y A, Rud’ V Y, Rud’ Y V and Terukov E I 2009 Tech. Phys. 54 1597-601 https://doi.org/10.1134/S1063784209110073

11. Morozova V A, Marenkin S F and Koshelev O G 1999 Inorg. Mater. 35 661-3.

12. Marenkin S F, Morozova V A and Koshelev O G 2010 Inorg. Mater. 46 1001-6 https://doi.org/10.1134/S0020168510090153

13. Dovesi R, Erba A, Orlando R, Zicovich‐Wilson C M, Civalleri B, Maschio L, Rérat M, Casassa S, Baima J, Salustro S and Kirtman B 2018 WIREs Comput. Mol. Sci. 8 e1360 https://doi.org/10.1002/wcms.1360

14. Dovesi R, Saunders V R, Roetti C, Orlando R, Zicovich-Wilson C M, Pascale F, Civalleri B, Doll K, Harrison N M, Bush I J, D’Arco P, Llunell M, Causà M, Noël Y, Maschio L, Erba A, Rérat M and Casassa S 2017 CRYSTAL17 User’s Manual (University of Torino).

15. Perdew J P, Ruzsinszky A, Csonka G I, Vydrov O A, Scuseria G E, Constantin L A, Zhou X and Burke K 2008 Phys. Rev. Lett. 100 136406 https://doi.org/10.1103/PhysRevLett.100.136406


J.Con.Ma 2023;1(2)131
S Rajpurohit et al: Ab-initio Investigation of Elastic Properties of Monoclinic ZnAs2 Crystal

16. Monkhorst H J and Pack J D 1976 Phys. Rev. B 13 5188-92 https://doi.org/10.1103/PhysRevB.13.5188

17. Broyden C G 1965 Math. Comput., 19 577-93 https://doi.org/10.2307/2003941

18. Johnson D D 1988 Phys. Rev. B 38 12807-13 https://doi.org/10.1103/PhysRevB.38.12807

19. Perger W F, Criswell J, Civalleri B and Dovesi R 2009 Comput. Phys. Commun. 180 1753-9 https://doi.org/10.1016/j.cpc.2009.04.022

20. Erba A, Mahmoud A, Orlando R and Dovesi R 2014 Phys. Chem. Minerals 41 151-60 https://doi.org/10.1007/s00269-013-0630-4

21. Gaillac R, Pullumbi P and Coudert F X 2016 J. Phys.: Condens. Matter, 28 275201 https://doi.org/10.1088/0953-8984/28/27/275201

22. http://progs.coudert.name/elate

23. Nye J F 1985 Physical Properties of Crystals: Their Representation by Tensors and Matrices (New York: Oxford University Press) chapter VIII (Elasticity. Fourth-Rank Tensors)

24. Balazuk V N, Bogachev G U, Kuryachii V Y, Marenkin S F, Mihalchenko V P, Pishikov D I and Rarenko A I 1982 Solid State Phys. (in Russian) 33 2777

25. Voigt W 1928 Lehrbuch der Kristallphysik (Leipzig: B G Teubner)

26. Reuss A and Angew Z 1929 Math. Mech. 9 49–58

27. Hill R 1952 Proc. Phys. Soc. A 65 349–54 https://doi.org/10.1088/0370-1298/65/5/307

28. Pugh S F 1954 Phil. Mag. 45 823–43 https://doi.org/10.1080/14786440808520496

29. Love A E H 1944 A Treatise on the Mathematical Theory of Elasticity (New York: Dover)

30. Chung D H and Buessem W R 1967 J. Appl. Phys. 38 2010–2 https://doi.org/10.1063/1.1709819

31. Chung D H and Buessem W R 1968 Anisotropy in Single-Crystal Refractory Compounds vol 2, ed F W Vahldiek and S A Mersol (New York: Plenum Press) p 217–48

32. Ranganathan S I and Ostoja-Starzewski M 2008

Phys. Rev. Lett. 101 055504 https://doi.org/10.1103/PhysRevLett.101.055504


J.Con.Ma 2023;1(2)132