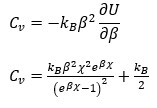E-ISSN:2583-9152

Research Article

Material Science

Journal of Condensed Matter

2023 Volume 1 Number 2 Jul-Dec
Publisherwww.thecmrs.in

Thermodynamic Properties of Polar Quantum Disc with Conical Disclination

Saklani R1, Kaushikb B2, Pratap S3*
DOI:10.61343/jcm.v1i02.24

1 Ritik Saklani, Department Of Physics Astronomical Science, Central University Of Himachal Pradesh 176206, Hp, India.

2 Bhavya Kaushikb, Department Of Physics Astronomical Science, Central University Of Himachal Pradesh 176206, Hp, India.

3* Surender Pratap, Department Of Physics Astronomical Science, Central University Of Himachal Pradesh 176206, HP, India.

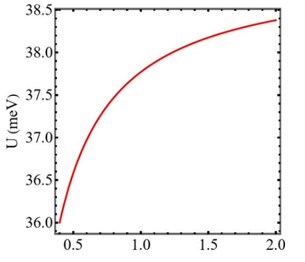
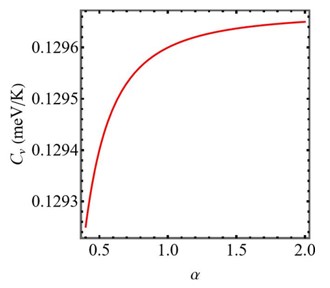
In this study, we have investigated the thermodynamic properties of the polar quantum disc having conical disclination. The spectrum of the non-interacting charged particle system was obtained with the aid of the Schrödinger equation with the effective mass approximation. The charged particle under investigation is confined by parabolic potential and a homogeneous magnetic field perpendicular to the quantum disc. We have shown the variation of internal energy (U) and specific heat Cv with the kink parameter α. Both U and Cv increase with the increase in α.

Keywords: Specific heat, Polar Quantum Disc, Internal energy, Thermodynamic Properties.

Corresponding Author How to Cite this Article To Browse
Surender Pratap, , Department Of Physics Astronomical Science, Central University Of Himachal Pradesh 176206, , HP, India.
Email: 		Saklani R, Kaushikb B, Pratap S, Thermodynamic Properties of Polar Quantum Disc with Conical Disclination. J.Con.Ma. 2023;1(2):133-137.
Available From
https://jcm.thecmrs.in/index.php/j/article/view/24

Manuscript Received Review Round 1 Review Round 2 Review Round 3 Accepted
2023-11-10 2023-11-15 2023-11-20 2023-11-25 2023-12-01
Conflict of Interest Funding Ethical Approval Plagiarism X-checker Note
None Nil Yes 21.90%

© 2023by Saklani R, Kaushikb B, Pratap Sand Published by Condensed Matter Research Society. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/ unported [CC BY 4.0].

J.Con.Ma 2023;1(2)133
Original Article Saklani et al: Thermodynamic Properties of Polar Quantum Disc

Introduction

The quest for low-dimensional materials rapidly increasing day by day after the successful synthesis of two-dimensional (2D) graphene [1]. The discovery of 2D graphene has opened up new avenues in the fundamental science and technology of low-dimensional materials [2,3]. Many of graphene's extraordinary features stem from its dimensionality and exceedingly unusual electronic dispersion relation, in which electrons imitate relativistic particles. The electrons in graphene are usually referred to as massless Dirac fermions, which may be thought of as electrons with zero rest mass (despite the fact that electrons are fundamental particles with characteristic mass) [4]. As a result, the unusual behavior of electrons makes graphene an ideal material to explore relativistic effects in condensed matter physics. The most remarkable consequences of the unusual behavior of electrons in graphene are the quantum Hall effect, anomalous quantum Hall effect, Klein paradox, ballistic electron propagation, metal-free magnetism, breakdown of the adiabatic Born-Oppenheimer approximation, possibility of high TC superconductivity, and observation of relativistic phenomena such as zitterbewegung or jittery motion of a wave function under the influence of confining potentials [1].

In graphene, the inherent binary degrees of freedom, such as valleys, sublattices, and top/bottom layers in multilayers, result in a 2D electron gas with valley selective chirality of the electrons at the Fermi energy. As a result, breaking the spatial inversion symmetry through staggered AB sublattice potentials in graphene or applying a vertical electric field in rhombohedral multilayers opens up a band gap [4]. Moreover, 2D graphene is naturally anticipated to include 1D zero-line modes caused by kinks in the Dirac mass [5]. Recently, Bi et al. investigated the role of topological defects on the electronic and transport properties of zero-line modes in single and bilayer graphene systems. The band evolution of the quantum valley Hall edge modes and the zero-line modes in bilayer graphene ribbons reveals that the edge modes of the quantum valley Hall effect develop changing gaps as the ribbon orientation deviates from the zigzag direction, whereas the corresponding zero-line modes remain gapless all the way except in the armchair direction [6].

The study of edge states in graphene structures is currently gaining popularity. It has been discovered that zigzag graphene nanoribbons (ZGNRs) have a localized edge state near the Fermi energy, which has a significant impact on their electronic behavior [7]. In ZGNRs, the existence of edge states results in zero energy band gap, and hence these nanoribbons are always metallic [7,8]. Because the presence of an energy gap is required for many applications in nanoelectronics, controlling and manipulating the edge states in ZGNRs is a significant problem [8]. The effect of external electric potentials applied along the edges of ZGNR can produce a spectral gap, transforming the metallic behavior of ZGNR to a semiconducting one. Therefore, it has been observed that edge states are sensitive to external electric potentials and are topological in nature [9,10]. The topological defects present in the system have crucial effects on the physical properties of the system under investigation. The presence of topological defects can modify the electronic, thermal, and thermodynamic properties of the material [11]. In this study, we theoretically investigated the thermodynamic properties of the polar quantum disc with conical disclination within the presence of a uniform magnetic field . We have considered the parabolic electric potential for confinement in the polar disc. The Volterra process is used to introduce the disclination defect [12]. The partition function (Z) of the system is obtained after solving the Schrödinger equation with the effective mass approximation. The conical disclination described by the Volterra process is depicted in figure 1.

jcm_24_01.jpg
Figure 1: Volterra Construction for the polar quantum disc in which a sector is removed from the disc. The vertical arrow represents homogeneous magnetic field.

Theoretical Formulation

We have considered a polar quantum disc of radius R and height h with a topological defect in


J.Con.Ma 2023;1(2)134
Original Article Saklani et al: Thermodynamic Properties of Polar Quantum Disc

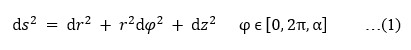
the form of conical disclination in the presence of a uniform magnetic field. The disclinated disc follows the metric given below:jcm_24_02.jpg
where α is the kink parameter which is related to the deficit angle (for 0 < α <1) or surplus angle (for α >1). Disc having no conical disclination is associated with kink parameter value α equal to one. We simplify the metric using the following transformation of coordinate system [12].
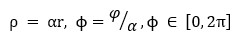jcm_24_03.jpg    …(2)the simplified metric has the form
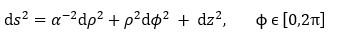jcm_24_04.jpg    …(3)

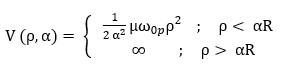The parabolic potential for the polar disc is defined as:jcm_24_05.jpg …(4)
The potential in the axial direction is
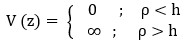
jcm_24_06.jpg
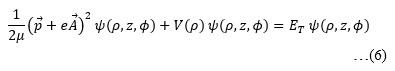
where, μ represents the electron’s effective mass, while ω0p corresponds to the angular frequencies linked with the classical harmonic oscillator for the parabolic potential. The Schrödinger equation in effective mass approximation is written as [13]-jcm_24_07.jpg
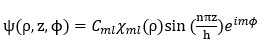where p= -ihΔ. is the quantum mechanical momentum operator and A=(BP/2Α)is the vector potential with the magnetic field. Total wavefunction for electron in polar quantum disc can be written in the form:jcm_24_08.jpg  …(7)
where Cml is the normalization factor, which depends on the values of the azimuthal m and radial l quantum numbers. The radial part of the electron’s wavefunction satisfies a second order differential equation:
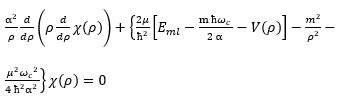
jcm_24_09.jpg
The solution of the radial Schrödinger equation is

a linear combination of the Whittaker M and W functions

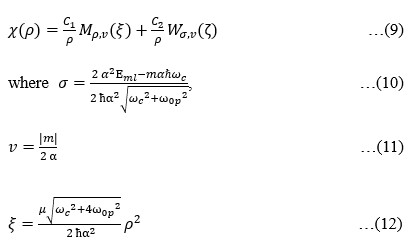jcm_24_10.jpg  ,                                 
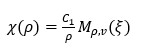C1 and C2 are constants. In Eqn. (9), the Whittaker W function has divergent nature at origin, so C2 = 0, leaving the radial component of the wave function a  jcm_24_11.jpg …(13)
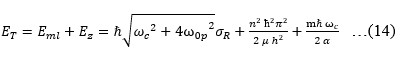
Also, the electron’s wave function must vanish at boundary of the wall (ρ = αR) and we obtained the following expression for the energy eigen valuejcm_24_12.jpg 
in which σR is the value of σ that satisfies the boundary condition Mσ,ν(ζR) = 0, with ζR = ζ (ρ =  αR).

The partition function is given by
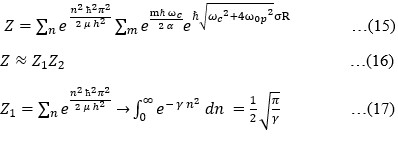
jcm_24_13.jpg
where , and we have used the classical approximation because the order of spacing between the energy level is very less than the thermal energy that is Δ E ≈ 10-42 J << kB T ≈ 10-21 J, so we have replaced summation with the integration.
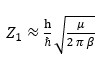jcm_24_14.jpg …(18)
where h is the height of disc.

Now,


J.Con.Ma 2023;1(2)135
Original Article Saklani et al: Thermodynamic Properties of Polar Quantum Disc

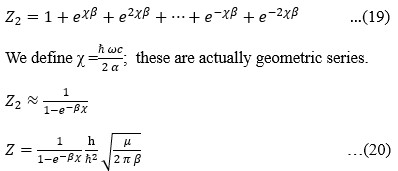
jcm_24_15.jpg 

We define χ = ;  these are actually geometric series.

Internal energy U is given by:
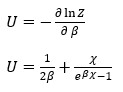jcm_24_16.jpg    …(21)
Specific heat is given by
jcm_24_17.jpg

Results and Discussion

jcm_24_18.jpg
Figure 2: Variation of internal energy U with the kink parameter α for polar quantum disc with disclination.

In our calculations, we have taken the effective mass of electron μ = 0.067 me, magnetic energy ̄ħωc = 5.0 meV, thermal energy (kBT) = 26 meV, and temperature (T) = 300 K. Figures 2 and 3 show the variation of internal energy and specific heat capacity with the kink parameter (α) of a polar quantum disc with conical disclination. It is clear from figure 2 that for α < 1, the increase in internal energy is very sharp, whereas, for α > 1, the internal energy slowly increases

and approaches a constant value. Hence, in the presence of a uniform magnetic field, the internal energy of the system is enhanced due to the distortion produced by disclination.

For α < 1, and T = 300 K, the Cv sharply increases with a small increase in α (see figure 3). For α > 1 with the same temperature, Cv increases with α and becomes constant at higher values of α > 1.5.


Figure 3: Variation of specific heat Cv with kink parameter α for polar quantum disc having disclination.

Conclusion

We investigated a theoretical study to calculate the internal energy & specific heat for a polar quantum disc with conical disclination. The charge particle in quantum disc is confined by parabolic electric potential in the presence of the homogeneous magnetic field perpendicular to plan of polar quantum disc. Results show that internal energy and specific heat can be modulated with the kink parameter. These findings are crucial for the design of nanodevices.

Acknowledgement

Authors wish to acknowledge the Central University of Himachal Pradesh for providing the facility during the course of this work.

References

1. A. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov, and A. K. Geim, “The electronic properties of graphene,” Reviews of modern physics 81, 109 (2009).


J.Con.Ma 2023;1(2)136
Original Article Saklani et al: Thermodynamic Properties of Polar Quantum Disc

2. S. Kumar, S. Pratap, V. Kumar, R. K. Mishra, J. S. Gwag, and B. Chakraborty, “Electronic, transport, magnetic, and optical properties of graphene nanoribbons and their optical sensing applications: A comprehensive review,” Luminescence 38, 909–953 (2023).

3. S. Pratap, N. Joshi, R. Trivedi, C. S. Rout, B. Chakraborty, et al., “Recent development of two-dimensional tantalum dichalcogenides and their applications,” Micro and Nanostructures, 207627 (2023).

4. H. Min, B. Sahu, S. K. Banerjee, and A. MacDonald, “Ab initio theory of gate induced gaps in graphene bilayers,” Physical Review B 75,155115 (2007).

5. W. Yao, S. A. Yang, and Q. Niu, “Edge states in graphene: From gapped flat-band to gapless chiral modes,” Physical review letters 102, 096801 (2009).

6. X. Bi, J. Jung, and Z. Qiao, “Role of geometry and topological defects in the one-dimensional zero-line modes of graphene,” Physical Review B 92, 235421 (2015).

7. S. Pratap, “Transport properties of zigzag graphene nanoribbons in the confined region of potential well,” Superlattices and Microstructures 100, 673–682 (2016).

8. S. Pratap, S. Kumar, and R. P. Singh, “Certain aspects of quantum transport in zigzag graphene nanoribbons,” Frontiers in Physics 10, 940586 (2022).

9. P. Delplace, D. Ullmo, and G. Montambaux, “Zak phase and the existence of edge states in graphene,” Physical Review B 84, 195452 (2011).

10. C. K. Chiu, J. C. Teo, A. P. Schnyder, and S. Ryu, “Classification of topological quantum matter with symmetries,” Reviews of Modern Physics 88, 035005 (2016).

11. S. Fumeron, B. Berche, F. Moraes, F. A. Santos, and E. Pereira, “Geometrical optics limit of phonon transport in a channel of disclinations,” The European Physical Journal B 90, 1–8 (2017).

12. J. D. Castano-Yepes, D. Amor-Quiroz, C. Ramirez-Gutierrez, and E. A. Gómez, “Impact of a topological defect and rashba spin-orbit interaction on the thermo-magnetic and optical properties

of a 2d semiconductor quantum dot with gaussian confinement,” Physica E: Low-dimensional Systems and Nanostructures 109, 59–66 (2019).

13. C. Furtado, B. G. da Cunha, F. Moraes, E. B. de Mello, and V. Bezzerra, “Landau levels in the presence of disclinations,” Physics Letters A 195, 90–94 (1994).


J.Con.Ma 2023;1(2)137