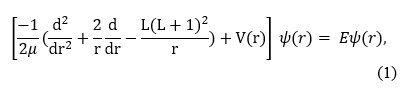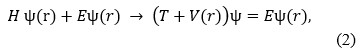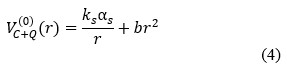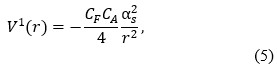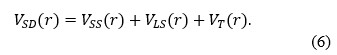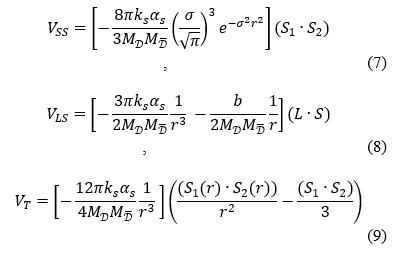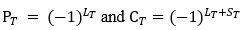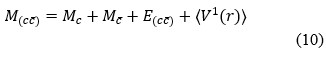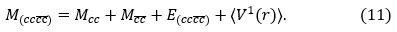E-ISSN:2583-9152

Research Article

Applied Physics

Journal of Condensed Matter

2023 Volume 1 Number 2 Jul-Dec
Publisherwww.thecmrs.in

All Charm Tetraquark Spectra in Coulombic Plus Quadratic Potential

Lodha C1*, Oudichhya J2, Tiwari R3, Rai A4
DOI:10.61343/jcm.v1i02.23

1* Chetan Lodha, Department Of Physics, Sardar Vallabhbhai National Institute Of Technology, Surat, Gujarat 395007, India.

2 Juhi Oudichhya, Department of Physics, Sardar Vallabhbhai National Institute of Technology, Surat, Gujarat 395007, India.

3 Rohit Tiwari, Department of Physics, Sardar Vallabhbhai National Institute of Technology, Surat, Gujarat 395007, India.

4 Ajay Kumar Rai, Department of Physics, Sardar Vallabhbhai National Institute of Technology, Surat, Gujarat 395007, India.

A non-relativistic model with relativistic corrections is used to generate the mass spectra of all charm tetraquark in the diquark-antidiquark system. Fitting parameters are derived by numerically solving the Schrodinger equation for the charmonium meson using the coulombic potential and the harmonic confinement interaction potential. The mass spectra of all charm tetraquark is calculated in present work by systematically reducing a four-body problem to a two-body problem using the parameters obtained from charmonium spectra.

Keywords: High Energy Physics, Tetraquark, Quark, Diquark, Potential Model, Exotic Hadrons.

Corresponding Author How to Cite this Article To Browse
Chetan Lodha, Department Of Physics, Sardar Vallabhbhai National Institute Of Technology, Surat, Gujarat 395007, India.
Email: 		Lodha C, Oudichhya J, Tiwari R, Rai A, All Charm Tetraquark Spectra in Coulombic Plus Quadratic Potential. J.Con.Ma. 2023;1(2):185-190.
Available From
https://jcm.thecmrs.in/index.php/j/article/view/23

Manuscript Received Review Round 1 Review Round 2 Review Round 3 Accepted
2023-11-10 2023-11-15 2023-11-20 2023-11-25 2023-12-01
Conflict of Interest Funding Ethical Approval Plagiarism X-checker Note
None Nil Yes 21.98%

© 2023by Lodha C, Oudichhya J, Tiwari R, Rai Aand Published by Condensed Matter Research Society. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/ unported [CC BY 4.0].

J.Con.Ma 2023;1(2)185
Lodha et al: Charm Tetraquark Spectra in Coulombic Plus Quadratic Potential

Introduction

Since 1964, when Gell-Mann proposed the component quark model [1], a considerable number of conventional hadrons, notably baryons and mesons, have been experimentally detected [2-4]. Other exotic states, such as the tetraquark, pentaquark, hybrid meson, mesonic molecule, and so on, were postulated a few years later [5-8], and the realm of exotic particle physics has witnessed great theoretical and experimental progress in the last several decades. In the last decade, experimental facilities including as Belle, CDF, D∅, CMS, LHCb, BABAR, CDF, and BESIII have discovered a plethora of candidates for exotic hadrons [9-12]. Since the first tetraquark candidate was proposed in 2003 at Belle [13], physicists all around the planet have been attempting to explain the mass and structure of these hadrons.

In 2007, Belle observed the Z (4430) state with a quark content of  [14]. Another state, Y (4660), has also shown the indications of tetraquarks [14]. Following these discoveries, in 2009, Fermilab observed Y (4140), which decays into J/ψ and ϕ mesons and is reasoned to have charm and anti-charm content with a probable four quark combination [15]. The first confirmed four quark state was revealed in 2013 by BES III, the Zc (3900), which decays into a charged pions π± and a J/ψ meson [16]. Since 2016, LHCb has identified ten new additional tetraquark candidates, with the notable discovery of the all-charm tetraquark   resonance X (6900) [15, 17-19].

The naming scheme of exotic hadrons is an extension of the XYZ states, which are used for heavy mesons. Following the convention, the neutral charmonium like exotic states that are observed in hadronic decays are regarded as X states. The Y states are neutral charmonium like exotic states observed in e+e− collisions with JPC value: 1− −. Lastly, the Z states are the charged, charmonium like exotic states [20].

Mesons have helped scientists understand the behavior of the strong force and the structure of atomic nuclei, their mass spectra become very significant. Considering the fact that mesons are one of the more primitive two-body systems in QCD, several theoretical models have been employed to calculate their mass spectra [21-27]. Similarly, many theoretical approaches like lattice

QCD [28], QCD sum rules [29], NRQCD [30-31], and some potential models [32-33] are being used to explain these tetraquarks. Numerous studies also explain a four-quark state as a hadronic molecular state [34-38]. By comparing the different theoretical predictions for the mass spectrum of tetraquark states with the experimental evidence, we may be able to gain a better understanding of the mechanics of strong interactions.

The primary goal of the present work is to look into the heavy-heavy tetraquark sector. In our previous studies [39-43], the well-known Cornell Potential has been employed and several tetraquarks have been calculated. In this work, we have used a similar approach but with modifications in confinement potential. The acquired masses have been compared with two meson thresholds. The paper is organized as follows: after a brief introduction in Section 1, Section 2 describes the diquark-antidiquark formalism and the mass spectra generated by this formalism for charmonium mesons and all charm tetraquarks. Section 3 summarizes the results and a discussion, and Section 4 discusses the study’s prospects for future research.

Experimental

High energy potential phenomenology has inspired various potential models that compute constituent quark interaction in a non-relativistic framework. Typically, these quark interactions are determined using Lattice QCD and the QCD Sum Rule. Given that the kinetic energy of the constituent quarks of an all heavy tetraquark is reasonably small in comparison to their rest mass energy, a non-relativistic model in a static potential approach appears to be fairly advantageous [44]. The binding energy of each state is computed using the presented method by solving the time-independent radial Schrodinger wave equation [45] of the relevant state given by,
where, the orbital Quantum Number and eigenvalue of energy are denoted by L and E respectively. For a quark-antiquark interaction, the simplified Hamiltonian equation can be given by   


J.Con.Ma 2023;1(2)186
Lodha et al: Charm Tetraquark Spectra in Coulombic Plus Quadratic Potential


where constituent kinetic energy and interaction potential are given by T and V(r) receptively. In a two body, center of mass frame, the fundamental Hamiltonian for tetra quarks and mesons with constituent mass Mi, relative momentum of the system pi and interaction potential V(r) is given by, 
The potential employed in this study is made up of coulombic potential and quadratic potential terms. The coulumbic component is caused by the Lorentz vector exchange, which is essentially one gluon exchange in this case; the quadractic word explains the confinement associated with the Lorentz scalar exchange.

Because the confinement component is quadratic, the potential energy grows quadratically with the distance between the quarks. The potential energy grows unbound as the separation between quarks increases. This forbids quarks from being separated or detected as free particles, but instead confines them within hadrons, generating color-neutral bound states. The quadratic confinement potential is comparable to the harmonic oscillator potential, although the exact nature of the confinement process in Quantum Chromodynamics is still unknown. The zeroth order potential in coulombic plus quadratic term is given by,

where the QCD running coupling constant, color factor and string tension are given by αs , ks and b respectively. In order to incorporate relativistic mass correction, term V1(r) is included which was originally established by Y. Koma et al. [46] in the central potential model. The leading-order perturbation theory yields the relativistic mass correction term V1(r) given as,     
where the Casimir charges of fundamental and adjoint representation are given by CF and CA respectively [46]. Spin dependent interaction is critical for understanding the splitting of radial and orbital excitations of mesons and tetraquarks for different quantum numbers. One gluon exchange is integrated utilizing the Briet Fermi Hamiltonian in

the first order perturbation theory [47]. This integration is done by adding the matrix components as an energy correction for spin-dependent interactions, given by
,
 The spin-orbit term VLS and the tensor term VT describe the fine structure of any given state [48]. At the same time, the spin-spin interaction term VSS, which is proportional to 2S1· S2, describes the hyperfine splitting [48]. These spin-dependent terms are defined as,

where MD and MD are the masses of constituents, namely quarks and antiquarks for mesons and diquarks and antidiquarks for tetraquarks. For the investigation of heavy quarkonium spectroscopy, σ parameter is substituted for the Delta function in the Briet Fermi Hamiltonian. For spin-1 diquarks and spin-1 antidiquarks, all the spin-dependent terms are computed, which combine to form the color singlet tetra quark with spin S = 0, 1 and 2. Coupling total spin ST with total orbital angular momentum LT results in total angular momentum JT. This coupling is used to obtain the mass spectra of radial and orbital excitations. JPC values are calculated using 

Results

1. Charmonium spectroscopy

The masses of diquarks and tetraquarks are calculated using the parameters obtained by J/ψ meson spectra. Since SU(3) color symmetry allows only colorless quark combination,  will exhibit  representation for mesons, which carries a color factor of ks =  [49]. The masses of  states are obtained by,


J.Con.Ma 2023;1(2)187
Lodha et al: Charm Tetraquark Spectra in Coulombic Plus Quadratic Potential


Inspired by previous studies, all parameters in this methodology are fixed by considering the mass spectra of mesons. Our present work utilizes four parameters (m,αs,b,σ) for tetraquark states model mass provided in the Table 1. Using this dataset, the mass spectra of charmonium and all charm tetraquark is obtained. Table 2 is the tabulation of the final mass spectra of cc.

Table 1: Parameters for calculating  Meson and   Tetraquark mass spectra.

αsb(GeV2)σ(GeV)mc(GeV)State
0.4250.0450.4751.45 

Table 2: Mass spectra of  Meson with various quantum number (MeV).

StateJPC⟨V1(r)⟩MassPDG [20][43]Meson
0S10− +-4.852982.272983.902983ηc(1S)
3S11− −-4.973004.733096.903075J/ψ(1S)
1P11+ −-4.103515.693525.373502hc(1P)
3P00+ +-3.673411.653414.713410χc0(1P)
3P11+ +-4.013527.353510.673492χc1(1P)
3P22+ +-4.103559.223556.173543χc2(1P)

2. All charm tetraquark spectroscopy

A pair of anti(quarks) interacting with each other via gluonic exchange forms a bound state, more commonly known as anti(diquark). Using the ground state diquarks(11S0) [cc], compact diquarks are calculated. Using the same methodology to calculate the mass of a meson, a (anti)diquark mass is calculated. For (anti)diquark the color factor ks due to QCD color symmetry in the antitriplet state is -2/3 which makes the short-distance interaction attractive [49]. Since it reduces a four-body problem into a two-body problem, the diquark-antidiquark approximation becomes central to this method. A diquark antidiquark pair held together by color forces constitutes a color singlet tetraquark. An all charm tetraquark in color singlet state has a color factor ks = −3/4 . The color singlet tetraquark can be represented as |QQ|3 [49]. Using the same formulation as in the case of the meson, tetraquark masses for many states are calculated, by namely;

Discussion

The Utilizing the zeroth order potential in form of coulombic plus quadratic term with relativistic mass correction, the mass spectra of charmonium and all charm tetraquark have been generated in the present work, as shown in table 2 and 3. The obtained results are compared with the masses

mentioned in Particle Data Group (PDG) [20] for the experimentally observed meson. Comparison with Cornell Potential model is also done and our masses show close proximity with other model as well as the experimentally observed masses. The S wave scalar meson and P wave scalar and Tensor meson are within 5 MeV mass difference from the observed mass [20], whereas vector meson in P wave and S wave are also very close to the experimentally observed states.

The masses for the all charm tetraquark are compared with other theoretical models [43] as well as with the two-meson threshold. The ground state tetraquark is only a few MeV below the two-meson threshold while other states also do not diverge far from the threshold. The calculated masses show comparable result with other models and will help providing useful information for future experimental as well as theoretical studies of tetraquarks and other exotic hadrons. We would like to use Regge phenomology for the determination of mass spectra of tetraquarks as it has already shown promising results in meson and baryon sector [50-54].

Table 3: Mass spectra of Tetraquark with various quantum number (MeV).

StateJPC⟨V1(r)⟩Mass[43]MThThreshold
0S10+ +-4.175955.7759395967.80ηc(1S) ηc(1S)
3S11+ −-4.045962.0459866080ηc(1S) J/ψ(1S)
5S22+ +-4.235975.1760796193.8J/ψ(1S) J/ψ(1S)
1P11− −-2.896448.336553--
3P00− +-2.976351.0464606398.61ηc(1S) χc0(1P)
3P11− +-2.896443.1765546494.57ηc(1S) χc1(1P)
3P22− +-2.976478.1765876540.07ηc(1S) χc2(1P)
5P10− −-2.896341.1964596509.27ηc(1S) hc(1P)
5P21− −-2.976459.2365776607.57J/ψ(1S) χc1(1P)
5P33− −-2.886511.6266236653.07J/ψ(1S) χc2(1P)

Conclusion

In the current work, we present the spectroscopic mass spectra of charmonium meson and all charm tetraquark in coulombic plus quadratic potential with relativistic mass correction. When compared with PDG masses for charmonium and two meson thresholds for tetraquark, the mass spectra show agreeable results. The decay properties and tetraquark mass spectra with multiple flavored quarks will be generated in our future work.

References

1. M. Gell-Mann, Physics Letters 8, 214–215 (1964).

2. T. Lesiak (Belle), AIP Conf. Proc. 814, 493–497 (2006).


J.Con.Ma 2023;1(2)188
Lodha et al: Charm Tetraquark Spectra in Coulombic Plus Quadratic Potential

3. N. Brambilla, S. Eidelman, C. Hanhart, A. Nefediev, C.-P. Shen, C. E. Thomas, A. Vairo, and C.-Z. Yuan, Phys. Rept. 873, 1–154 (2020).

4. A. V. Berezhnoy, A. K. Likhoded, A. V. Luchinsky, and A. A. Novoselov, Phys. Rev. D 84, p. 094023 (2011).

5. D. B. Lichtenberg, E. Predazzi, D. H. Weingarten, and J. G. Wills, Phys. Rev. D 18, p. 2569 (1978).

6. R. L. Jaffe, Phys. Rev. D 15, p. 267 (1977).

7. R. L. Jaffe, Phys. Rev. Lett. 38, 195–198 (1977).

8. C. Gignoux, B. Silvestre-Brac, and J. M. Richard, Phys. Lett. B 193, p. 323 (1987).

9. R. F. Lebed, R. E. Mitchell, and E. S. Swanson, Prog. Part. Nucl. Phys. 93, 143–194 (2017).

10. S. L. Olsen, T. Skwarnicki, and D. Zieminska, Rev. Mod. Phys. 90, p. 015003 (2018).

11. A. Ali, J. S. Lange, and S. Stone, Prog. Part. Nucl. Phys. 97, 123–198 (2017).

12. A. Esposito, A. Pilloni, and A. D. Polosa, Phys. Rept. 668, 1–97 (2017).

13. S. K. Choi et al. (Belle), Phys. Rev. Lett. 91, p. 262001 (2003).

14. G. Cotugno, R. Faccini, A. D. Polosa, and C. Sabelli, Phys. Rev. Lett. 104, p. 132005 (2010).

15. R. Aaij et al. (LHCb), Phys. Rev. Lett. 118, p. 022003 (2017).

16. M. Ablikim et al. (BESIII), Phys. Rev. Lett. 115, p. 112003 (2015).

17. R. Aaij et al. (LHCb), Phys. Rev. D 95, p. 012002 (2017).

18. R. Aaij et al. (LHCb), Sci. Bull. 65, 1983–1993 (2020).

19. R. Aaij et al. (LHCb), Phys. Rev. Lett. 127, p. 082001 (2021).

20. R. L. Workman et al. (Particle Data Group), PTEP 2022, p. 083C01 (2022).

21. J. Oudichhya, K. Gandhi, and A. K. Rai, Phys. Rev. D 108, p. 014034 (2023).

22. V. Kher and A. K. Rai, Chin. Phys. C 42, p. 083101 (2018).

23. V. Kher, N. Devlani, and A. K. Rai, Chin. Phys. C 41, p. 093101 (2017).

24. V. Kher, N. Devlani, and A. K. Rai, Chin. Phys. C 41, p. 073101 (2017).

25. A. K. Rai, B. Patel, and P. C. Vinodkumar, Phys. Rev. C 78, p. 055202 (2008).

26. R. Chaturvedi and A. K. Rai, Eur. Phys. J. A 58, p. 228 (2022).

27. K. R. Purohit, P. Jakhad, and A. K. Rai, Phys. Scripta 97, p. 044002 (2022).

28. M. Wagner, A. Abdel-Rehim, C. Alexandrou, M. Dalla Brida, M. Gravina, G. Koutsou, L. Scorzato, and C. Urbach, J.
Phys. Conf. Ser. 503, p. 012031 (2014).

29. W. Chen, H.-X. Chen, X. Liu, T. G. Steele, and S.-L. Zhu, Phys. Lett. B 773, 247–251 (2017).

30. Z. Ghalenovi and M. M. Sorkhi, Eur. Phys. J. Plus 135, p. 399 (2020).

31. S. Noh and W. Park, Phys. Rev. D 108, p. 014004 (2023).

32. H. Mutuk, Eur. Phys. J. C 83, p. 358 (2023).

33. P. G. Ortega, J. Segovia, D. R. Entem, and F. Fernandez, Phys. Lett. B 841, p. 137918 (2023).

34. A. K. Rai, J. N. Pandya, and P. C. Vinodkumar, Indian J. Phys. A 80, 387–392 (2006).

35. D. P. Rathaud and A. K. Rai, Eur. Phys. J. Plus 132, p. 370 (2017).

36. D. P. Rathaud and A. K. Rai, Indian J. Phys. 90, 1299–1305 (2016).

37. A. K. Rai and D. P. Rathaud, Eur. Phys. J. C 75, p. 462 (2015).

38. A. K. Rai, J. N. Pandya, and P. C. Vinodkummar, Nucl. Phys. A 782, 406–409 (2007).

39. R. Tiwari and A. K. Rai, DAE Symp. Nucl. Phys. 66, 833–834 (2023).

40. R. Tiwari and A. K. Rai, Few Body Syst. 64, p. 20 (2023).

41. R. Tiwari, J. Oudichhya, and A. K. Rai, “Mass-spectra of light-heavy tetraquarks,” arXiv:2205.00679 .

42. R. Tiwari, D. P. Rathaud, and A. K. Rai, Eur. Phys. J. A 57, p. 289 (2021).

43. R. Tiwari, D. P. Rathaud, and A. K. Rai, Indian J. Phys. 97, 943–954 (2023).


J.Con.Ma 2023;1(2)189
Lodha et al: Charm Tetraquark Spectra in Coulombic Plus Quadratic Potential

44. E. Eichten, K. Gottfried, T. Kinoshita, K. D. Lane, and T.-M. Yan, Phys. Rev. D 21, p. 203 (1980).

45. S. Godfrey and N. Isgur, Phys. Rev. D 32, 189–231 (1985).

46. Y. Koma, M. Koma, and H. Wittig, Phys. Rev. Lett. 97, p. 122003 (2006).

47. M. B. Voloshin, Prog. Part. Nucl. Phys. 61, 455–511 (2008).

48. W. Lucha, F. F. Schoberl, and D. Gromes, Phys. Rept. 200, 127–240 (1991).

49. V. R. Debastiani and F. S. Navarra, Chin. Phys. C 43, p. 013105 (2019).

50. J. Oudichhya and A. K. Rai, Eur. Phys. J. A 59, p. 123 (2023).

51. J. Oudichhya, K. Gandhi, and A. K. Rai, Nucl. Phys. A 1035, p. 122658 (2023).

52. J. Oudichhya, K. Gandhi, and A. K. Rai, Phys. Scripta 97, p. 054001 (2022).

53. J. Oudichhya, K. Gandhi, and A. K. Rai, Phys. Rev. D 104, p. 114027 (2021).

54. J. Oudichhya, K. Gandhi, and A. K. Rai, Phys. Rev. D 103, p. 114030 (2021).

 


J.Con.Ma 2023;1(2)190