E-ISSN:2583-9152

Research Article

Material Science

Journal of Condensed Matter

2023 Volume 1 Number 2 Jul-Dec
Publisherwww.thecmrs.in

Transition Energy For a Polar Quantum Disc with Conical Disclination in Parabolic Confining Electric Potential

Kumar V1, Tshipa M2, Pratap S3*
DOI:10.61343/jcm.v1i02.21

1 Vinod Kumar, Department Of Physics Astronomical Science, Central University Of Himachal Pradesh, HP176206, India.

2 Moletlanyi Tshipa, University Of Botswana Private Bag 0022, Gaborone, Botswana.

3* Surender Pratap, Department Of Physics Astronomical Science, Central University Of Himachal Pradesh 176206, HP, India.

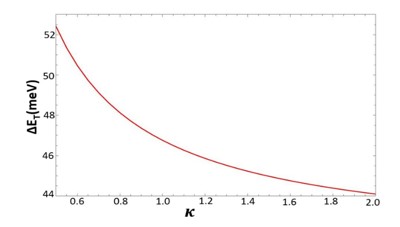
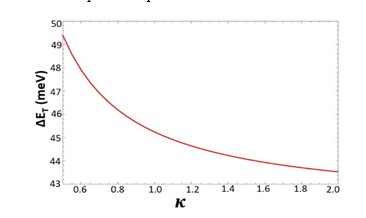
The Transition energy of an electron for a polar quantum disc with conical disclination is investigated theoretically. For charge carrier confinement, we consider the infinite polar square well potential (IPSW), and parabolic potential (PP). The disclination in the system is characterized by the kink parameter κ. The energy levels of the system were calculated using the Schrödinger equation with the effective mass approximation. Our study reveals that the transition energy decreases as the kink parameter κ increases.

Keywords: Transition energy, Conical disclination, Parabolic potentials, Quantum disc.

Corresponding Author How to Cite this Article To Browse
Surender Pratap, , Department Of Physics Astronomical Science, Central University Of Himachal Pradesh 176206, , HP, India.
Email: 		Kumar V, Tshipa M, Pratap S, Transition Energy For a Polar Quantum Disc with Conical Disclination in Parabolic Confining Electric Potential. J.Con.Ma. 2023;1(2):147-150.
Available From
https://jcm.thecmrs.in/index.php/j/article/view/21

Manuscript Received Review Round 1 Review Round 2 Review Round 3 Accepted
2023-11-10 2023-11-15 2023-11-20 2023-11-25 2023-12-01
Conflict of Interest Funding Ethical Approval Plagiarism X-checker Note
None Nil Yes 20.67%

© 2023by Kumar V, Tshipa M, Pratap Sand Published by Condensed Matter Research Society. This is an Open Access article licensed under a Creative Commons Attribution 4.0 International License https://creativecommons.org/licenses/by/4.0/ unported [CC BY 4.0].

J.Con.Ma 2023;1(2)147
Kumar et al.: Transition Energy Polar Quantum Disc with Conical Disclination Parabolic

Introduction

Over the past few decades, progress in nanotechnology and microfabrication methods has exposed a wide expanse of opportunities in the realm of low-dimensional systems [1- 2]. Low-dimensional systems exhibit quantum effects due to the restricted motion of their particles in a small region of space. These quantum effects are crucial for the design of nanodevices [3]. The confinement of particle motion in one, two-, and three-dimensions results in the formation of quantum wells, quantum wires, and quantum dots, respectively [4]. Quantum dots serve as miniature laboratories for conducting thorough tests of the predictions made by quantum mechanics [5]. Accurately describing a quantum dot relies on the precise form of the electric confinement potential. It is widely recognized that the harmonic potential serves as a suitable approximation, effectively capturing the fundamental traits of the quantum dot [6-7].  Advances in microfabrication techniques have made it possible to create quantum dots with a variety of geometries, such as spheres, cylinders, discs and so forth [8].

The behaviour of the system can be strongly influenced by topological defects, such as disclinations [9-10]. Topological defects are the defects in the system that cannot be removed by smooth continuous deformation [11]. Topological defects can be a source of variation in the electrical, acoustic, or thermal properties of material [12]. Disclination in a system can be best visualized by the Volterra construction [6], as shown in figure 1, in which a sector is removed from the disc or a segment is added into the polar disc.

jcm_21_1.jpg

Figure 1: Volterra Construction for the polar quantum disc in which a sector is removed from a disc [6].

Theoretical Formulation

Wavefunctions

The system under investigation is a polar quantum disc of radius R and height

h with a conical disclination. The disclination in the system is characterized by the kink parameter κ, where a value of κ less than 1 signifies the removal of a segment from the disc, and a value of κ greater than 1 represents the addition of a segment to the polar disc. When the kink parameter κ value is one implies that there is no disclination present in the system. Conical disclination modifies the metric of a disc from its otherwise Euclidean form as given below: 
    jcm_21_2.jpg
Coordinate transformation is used to make the metric simple for theoretical calculation as given below [6]. 
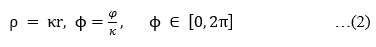
    jcm_21_3.jpg
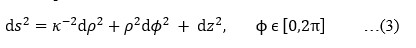
the simplified metric has the form    jcm_21_4.jpg
The parabolic potential for the polar disc is defined as:  jcm_21_5.jpg
The potential in the axial direction is 

where, μ represents the electron’s effective mass, while ω0p corresponds to the angular frequencies linked with the classical harmonic oscillator for the parabolic potential. In the context of the effective-mass approximation, the Schrödinger equation takes on the following form [13]-

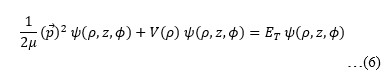
jcm_21_6.jpg
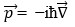where  is the quantum mechanical momentum operator with ħ = h/2π, in which h is Planck’s constant, i = √(−1), and ET is the total energy of the electron. For a single electron system in a polar quantum disc with an electric confining potential V(ρ), the wave function can be expressed as: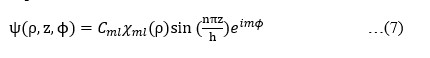jcm_21_7.jpg


J.Con.Ma 2023;1(2)148
Kumar et al.: Transition Energy Polar Quantum Disc with Conical Disclination Parabolic

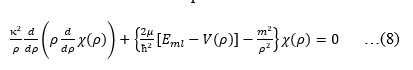
Cml where, C is the normalization constant, and m and l represent the azimuthal and radial quantum numbers, respectively. The total radial wave function of the electron χml (ρ), which assumes different forms depending on the radial electric potential V (ρ) being considered, satisfies the second-order differential equation jcm_21_8.jpg

Parabolic potential (PP)

The radial part of the wavefunction of a particle in a p arabolic potential can be expressed as a linear combination of two special functions, the Whittaker M and W functions.
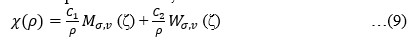
 (ζ) +  (ζ)                                  jcm_21_9.jpg  
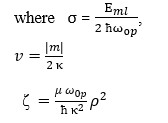
jcm_21_10.jpg
C1 and C2 are constants. In Eqn. (9), the Whittaker W function has to be discarded due to its divergent nature at the origin (ρ = 0), therefore C2 = 0, leaving the radial component of the wave function as
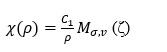
jcm_21_11.jpg                                   
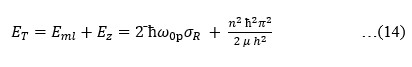
Requiring the vanishing of the wave function at the wall boundary (ρ = κR) and at the ends of the polar disc       leads to the following expression for the energy eigenvaluesjcm_21_12.jpg
in which σR is the value of σ that satisfies the boundary condition Mσ,ν (ζR) = 0, with ζR = ζ (ρ = κR) and Ez is simply the energy of a particle in a one dimensional box.

Infinite polar square well (IPSW)

The radial part of the wavefunction of a particle in an infinite square well potential can be expressed as a linear combination of BesselJ and BesselY functions as given below:

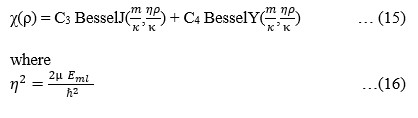
χ(ρ) = C3 BesselJ( , ) + C4 BesselY( , )          jcm_21_13.jpg
The second term in Eqn. (15) diverges at ρ = 0, so C4 is set to be zero. The energy eigenvalue for the infinite square potential well is given by the following expression:
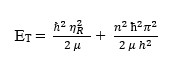
jcm_21_14.jpg
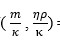The boundary condition BesselJjcm_21_14_a.jpg satisfied by the η represented by ηR.

Results and Discussion

Electrons in solids have an effective mass that is different from their mass in a vacuum. In our calculations we have taken the effective mass of electron μ = 0.067 me, the radius of disc R = 400 Å and the height of the disc h = 200Å. Figure 2 and 3 show the variation of total transition energy with kink parameter for a polar quantum disc having electric confining parabolic and infinite square well potential respectively. The higher the value of the kink parameter, the lower the transition energy becomes. As mentioned before, a kink parameter value less than 1 indicates a deficit angle, while a value greater than 1 indicates an additional angle introduced to the polar disc. When the kink parameter κ is less than 1, the confinement of electrons is stronger because they have less space to move. As κ increases, the space for electron movement also increases, making confinement weaker. As a result, confinement energy decreases with increasing kink parameter κ. Also, we noticed that the transition energy of the electron in the case of parabolic potential is higher than that of the infinite square well.

jcm_21_15.jpg
Figure 2: Variation of transition energy (m = 0 → m = 1) with kink parameter κ for parabolic potential


J.Con.Ma 2023;1(2)149
Kumar et al.: Transition Energy Polar Quantum Disc with Conical Disclination Parabolic

jcm_21_16.jpg
Figure 3: Variation of transition energy (m = 0 → m = 1) with kink parameter κ for infinite square well potential.

Conclusion

A theoretical study is made to calculate the transition energy for a polar quantum disc with conical disclination in electric confining parabolic and infinite square well potential. Results show that transition energy can be modulated via electric confining potential and kink parameters. These findings are crucial for the design of nanodevices.

Acknowledgement

We wish to acknowledge the Central University of Himachal Pradesh for providing the facility during the course of this work.

References

1. R. Ashoori, “Electrons in artificial atoms,” Nature 379, 413–419 (1996).

2. S. M. Reimann and M. Manninen, “Electronic structure of quantum dots,” Reviews of modern physics 74, 1283 (2002).

3. Moletlanyi Tshipa and Monkami Masale, “Optical transition rates in a cylindrical quantum wire with a parabolic and inverse parabolic electric confining potential in a magnetic field”, Optical and Quantum Electronics, 53:1-13, 2021.

4. S. Kumar D, J. Kumar B, and M. Matt, “Quantum nanostructures (quantum dots): An overview,” (2018) pp. 59–88.

5. B. Boyacioglu and A. Chatterjee, “Heat capacity and entropy of a gallium arsenide quantum dot with gaussian confinement,” Journal of applied physics 112, 083514 (2012).

6. J. D. Castaño-Yepes, D. Amor-Quiroz, C. Ramirez-Gutierrez, and E. A. Gómez, “Impact of a topological defect and rashba spin-orbit interaction on the thermo-magnetic and optical properties of a 2d semiconductor quantum dot with gaussian confinement,” Physica E: Low- dimensional Systems and Nanostructures 109, 59–66 (2019).

7. M. Tshipa, L. K. Sharma, and S. Pratap, “Photoionization cross-section in a gallium arsenide spherical quantum shell: the effect of parabolic confining electric potentials,” The European Physical Journal B 94, 129 (2021).

8. J. C. Foster, S. Varlas, B. Couturaud, Z. Coe, and R. K. O’Reilly, “Getting into shape: reflections on a new generation of cylindrical nanostructures’ self-assembly using polymer building blocks,” Journal of the American Chemical Society 141, 2742–2753 (2019.

9. V. Osipov, “Aharonov-bohm effect in planar systems with disclination vortices,” Physics Letters A 164, 327–330 (1992).

10. V. Bezerra, “Some remarks on loop variables, holonomy transformation, and gravitational aharonov-bohm effect,” Annals of Physics 203, 392–409 (1990).

11. A. Srivastava, “Topological defects in condensed matter physics,” in Field Theories in Condensed Matter Physics, Texts and Readings in Physical Sciences (Hindustan Book Agency, Gurgaon, 2001).

12. S. Fumeron, B. Berche, F. Moraes, F. A. Santos, and E. Pereira, “Geometrical optics limit of phonon transport in a channel of disclinations,” The European Physical Journal B 90, 1–8 (2017).

13. C. Furtado, B. G. da Cunha, F. Moraes, E. B. de Mello, and V. Bezzerra, “Landau levels in the presence of disclinations,” Physics Letters, 195(1):90–94, 1994.


J.Con.Ma 2023;1(2)150