A. Levy Yeyati, “Josephson and andreev transport through quantum dots”, Advances in Physics 60, 899 (2011).
6. D. Franceschi et al., “Hybrid superconductor–quantum dot devices”, Nature nanotechnology 5, 703 (2010).
7. Y. Zhu, Q.-f. Sun, and T.-h. Lin, “Andreev bound states and the π-junction transition in a superconductor/quantumdot/superconductor system”, Journal of Physics: Condensed Matter 13, 8783 (2001).
8. C. Karrasch, A. Oguri, and V. Meden, “Josephson current through a single anderson impurity coupled to bcs leads”, Physical Review B 77, 024517 (2008).
9. A. Dhyani, B. Tewari, et al., “Interplay of the single particle and josephson cooper pair tunneling on supercurrent across the superconducting quantum dot junction”, Physica E: Low-dimensional Systems and Nanostructures 42, 162
(2009).
10. J. A. Van Dam, Y. V. Nazarov, E. P. Bakkers, S. De Franceschi, and L. P. Kouwenhoven, “Supercurrent reversal in quantum dots”, Nature 442, 667 (2006).
11. Y. Ma, T. Cai, X. Han, Y. Hu, H. Zhang, H. Wang, L. Sun, Y. Song, and L. Duan, “Andreev bound states in a few-electron quantum dot coupled to superconductors”, Physical Review B 99, 035413 (2019).
12. D. Szombati, S. Nadj-Perge, D. Car, S. Plissard, E. Bakkers, and L. Kouwenhoven, “Josephson φ0-junction in nanowire quantum dots”, Nature Physics 12, 568 (2016).
13. S.-g. Cheng and Q.-f. Sun, “Josephson current transport through t-shaped double quantum dots”, Journal of Physics: Condensed Matter 20, 505202 (2008).
14. S. Droste, S. Andergassen, and J. Splettstoesser, “Josephson current through interacting double quantum dots with spin–orbit coupling”, Journal of Physics: Condensed Matter 24, 415301 (2012).
15. J. E. Saldana, A. Vekris, G. Steffensen, R. Zitko, P. Krogstrup, J. Paaske, K. Grove-Rasmussen, and J. Nygard, “Supercurrent in a double quantum dot”, Physical review letters 121, 257701 (2018).


 ©
© 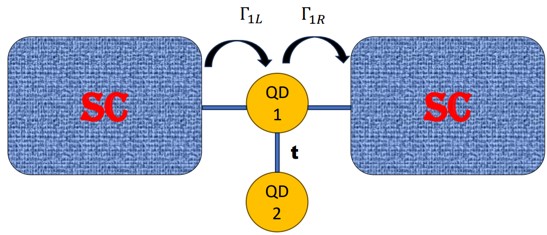
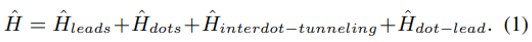
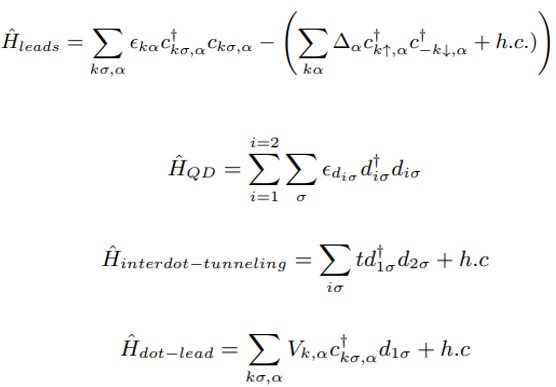
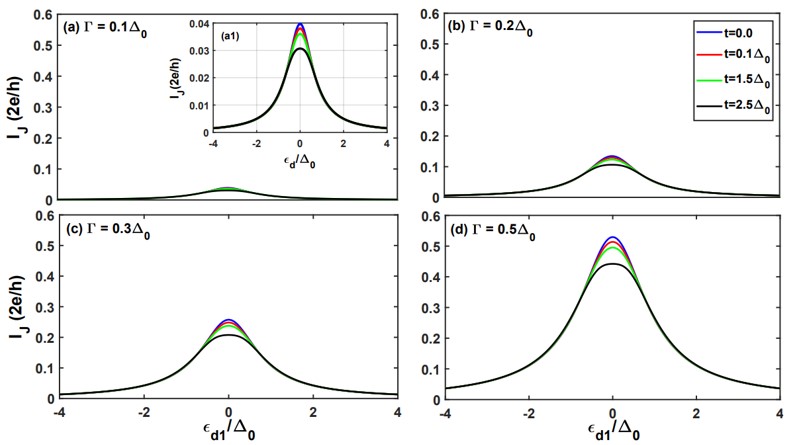
 is the Hamiltonian of BCS superconducting leads. In the first term ∈k∝ is the energy of superconducting leads (∝ ∈ L, R) and c†kσ,∝(ckσ,∝) is the creation (annihilation) operator of electrons with spin σ(↑,↓) and wave vector
is the Hamiltonian of BCS superconducting leads. In the first term ∈k∝ is the energy of superconducting leads (∝ ∈ L, R) and c†kσ,∝(ckσ,∝) is the creation (annihilation) operator of electrons with spin σ(↑,↓) and wave vector 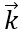 . The second term denotes the interaction between Cooper pairs where ∆∝ is the superconducting order parameter and is given as ∆∝ = |∆0|eiφ∝. denotes the Hamiltonian of double quantum dots. The energy of main quantum dot (QD1) and
. The second term denotes the interaction between Cooper pairs where ∆∝ is the superconducting order parameter and is given as ∆∝ = |∆0|eiφ∝. denotes the Hamiltonian of double quantum dots. The energy of main quantum dot (QD1) and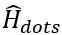 side quantum dot (QD2) is given by εdi with fermionic operators (d†iσ and diσ).
side quantum dot (QD2) is given by εdi with fermionic operators (d†iσ and diσ).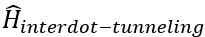 is the Hamiltonian for tunneling between both quantum dots and the amplitude of interdot tunneling is symbolized by t.
is the Hamiltonian for tunneling between both quantum dots and the amplitude of interdot tunneling is symbolized by t.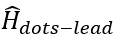 represents the hamiltonian for tunnelling between QD1 and superconducting leads where Vk,∝ is the tunneling strength between leads and QD1.
represents the hamiltonian for tunnelling between QD1 and superconducting leads where Vk,∝ is the tunneling strength between leads and QD1.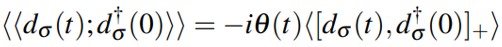
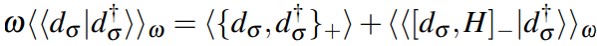 (2)
(2)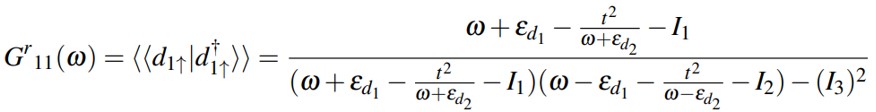 (3)
(3)